Chapter 3
Until now, all our procedures could be viewed as specifications for computing mathematical functions. A call to a procedure computed the value of the function applied to the given arguments, and two calls to the same procedure with the same arguments always produced the same result.
In general, programming with assignment forces us to carefully consider the relative orders of the assignments to make sure that each statement is using the correct version of the variables that have been changed. This issue simply does not arise in functional programs.11 The complexity of imperative programs becomes even worse if we consider applications in which several processes execute concurrently. We will return to this in section 3.4. First, however, we will address the issue of providing a computational model for expressions that involve assignment, and explore the uses of objects with local state in designing simulations.
substitution model of evaluation:
To apply a compound procedure to arguments, evaluate the body of the procedure with each formal parameter replaced by the corresponding argument.
Although the primitive objects of the constraint system are somewhat more complex, the overall system is simpler, since there is no concern about agendas and logic delays.
Sure it is. The time is always troublesome.
The term “mutex” is an abbreviation for mutual exclusion.
Oh I see.
3.1
3.1
(define (make-accumulator balance)
(lambda (amount)
(begin (set! balance
(+ balance amount))
balance)
))
3.2
(define (make-monitored f)
(let ((count 0))
(define (dispatch m)
(cond ((eq? m 'how-many-calls?) count)
((eq? m 'reset-count) (set! count 0))
(else (begin (set! count (+ count 1)) (f m) ))))
dispatch))
> (s 100)
10
> (s 'how-many-calls?)
1
> (s 100)
10
> (s 'how-many-calls?)
2
> (s 'how-many-calls?)
2
> (s 'how-many-calls?)
2
> (s 'reset)
sqrt: contract violation
expected: number?
given: 'reset
[,bt for context]
> (s 'reset-count)
> (s 'how-many-calls?)
0
> (s 100)
10
> (s 'how-many-calls?)
1
3.3
(define (make-account pass balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance
(- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch key m)
(cond ((not (eq? pass key)) "Incorrect password")
((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request:
MAKE-ACCOUNT" m))))
dispatch)
> ((acc 'secret-password 'withdraw) 40)
application: not a procedure;
expected a procedure that can be applied to arguments
given: "Incorrect password"
[,bt for context]
OK.
(define (make-account balance pass)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance
(- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request:
MAKE-ACCOUNT" m))))
(lambda (key m)
(if (eq? key pass)
(dispatch m)
(lambda (X) "Incorrect password")
)
)
)
3.4
LOL.
Can they combined together?
(define call-the-cops "COPS COMING")
(define (make-account balance pass)
(let ((try 0))
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance
(- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request:
MAKE-ACCOUNT" m))))
(lambda (key m)
(if (eq? key pass)
(dispatch m)
(begin
(set! try (+ try 1))
(if (> try 7)
(lambda (X) call-the-cops)
(lambda (X) "Incorrect password")
)
)
)
)
)
)
> (define acc
(make-account 100 'secret-password))
> ((acc 'secret-password 'withdraw) 40)
60
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"Incorrect password"
> ((acc 'some-other-password 'deposit) 50)
"COPS COMING"
> ((acc 'some-other-password 'deposit) 50)
"COPS COMING"
> ((acc 'some-other-password 'deposit) 50)
"COPS COMING"
3.5
Well, the MIT-Scheme is not the same as the racket, I need to rewrite random-in-range.
(define (random-in-range low high)
(let ((range (- high low)))
(+ low (random range))))
(define (estimate-integral P x1 x2 y1 y2 trials)
(* 4 (random-integral-test P x1 x2 y1 y2 trials)))
(define (random-integral-test P x1 x2 y1 y2 trials)
(define (iter trials-remaining trials-passed)
(let ((x (random-in-range x1 x2)))
(let ((y (random-in-range y1 y2)))
(cond ((= trials-remaining 0)
(/ trials-passed trials))
((P x y)
(iter (- trials-remaining 1)
(+ trials-passed 1)
))
(else
(iter (- trials-remaining 1)
trials-passed
))))))
(iter trials 0))
(define (get-pi trials)
(exact->inexact
(estimate-integral (lambda (x y)
(< (+ (square x)
(square y))
1.0))
-1.0
1.0
-1.0
1.0
trials)))
I could use the original monte-carlo, it seems much easier.
(define (estimate-integral p? x1 x2 y1 y2 trials) (* 4 (monte-carlo trials (lambda () (p? (random-in-range x1 x2) (random-in-range y1 y2))))))(define (get-pi trials) (exact->inexact (estimate-integral (lambda (x y) (< (+ (square x) (square y)) 1.0)) -1.0 1.0 -1.0 1.0 trials)))
3.6
We don’t have rand or rand-update in Racket. Oh, I find something: 2 SICP Language. OK, it still doesn’t work.
I guess it’s Just another dispatch.
(define rand
(let ((x random-init))
(define (dispatch message)
(cond ((eq? message 'generate)
(begin (set! x (rand-update x))
x))
((eq? message 'reset)
(lambda (new-value) (set! x new-value)))))
dispatch))
3.7
(define (make-account balance pass)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance
(- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request:
MAKE-ACCOUNT" m))))
(lambda (key m)
(if (eq? key pass)
(dispatch m)
(lambda (X) "Incorrect password")
)
)
)
(define (make-joint account old-pass new-pass)
(lambda (key m)
(if (eq? key new-pass)
(account old-pass m)
(error "Incorrect password" key)
)
)
)
The book said I may modify the 3.3 answer, while I just proxy it. There may be some better answer?
3.8
Wow, quite Interesting.
(define (f add)
(let ((a -1))
(begin (set! a (+ add))
a
)
)
)
This is another sign of referentially transparent.
> (define f (make-f))
> (f 0)
-1
> (f 1)
0
> (define f (make-f))
> (f 1)
0
> (f 0)
0
3.2
λ-expression was evaluated to produce the procedure
A procedure as a pair is created in an environment.
To apply a procedure to arguments, create a new environment containing a frame that binds the parameters to the values of the arguments. The enclosing environment of this frame is the environment specified by the procedure. Now, within this new environment, evaluate the procedure body.
The enclosing environment of this frame is the environment in which the procedure is created.
I wonder which part is frame and which is env. The body of the lambda (i.e. the pointers’ pair) is frame?
two key properties that make local procedure definitions a useful technique for modularizing programs:
- The names of the local procedures do not interfere with names external to the enclosing procedure, because the local procedure names will be bound in the frame that the procedure creates when it is run, rather than being bound in the global environment.
- The local procedures can access the arguments of the enclosing procedure, simply by using parameter names as free variables. This is because the body of the local procedure is evaluated in an environment that is subordinate to the evaluation environment for the enclosing procedure.
Will sqrt create a lot of env? There is a recursive call.
Since Scheme provides no way to mutate a symbol, this sharing is undetectable. Note also that the sharing is what enables us to compare symbols using
eq?, which simply checks equality of pointers.
3.9
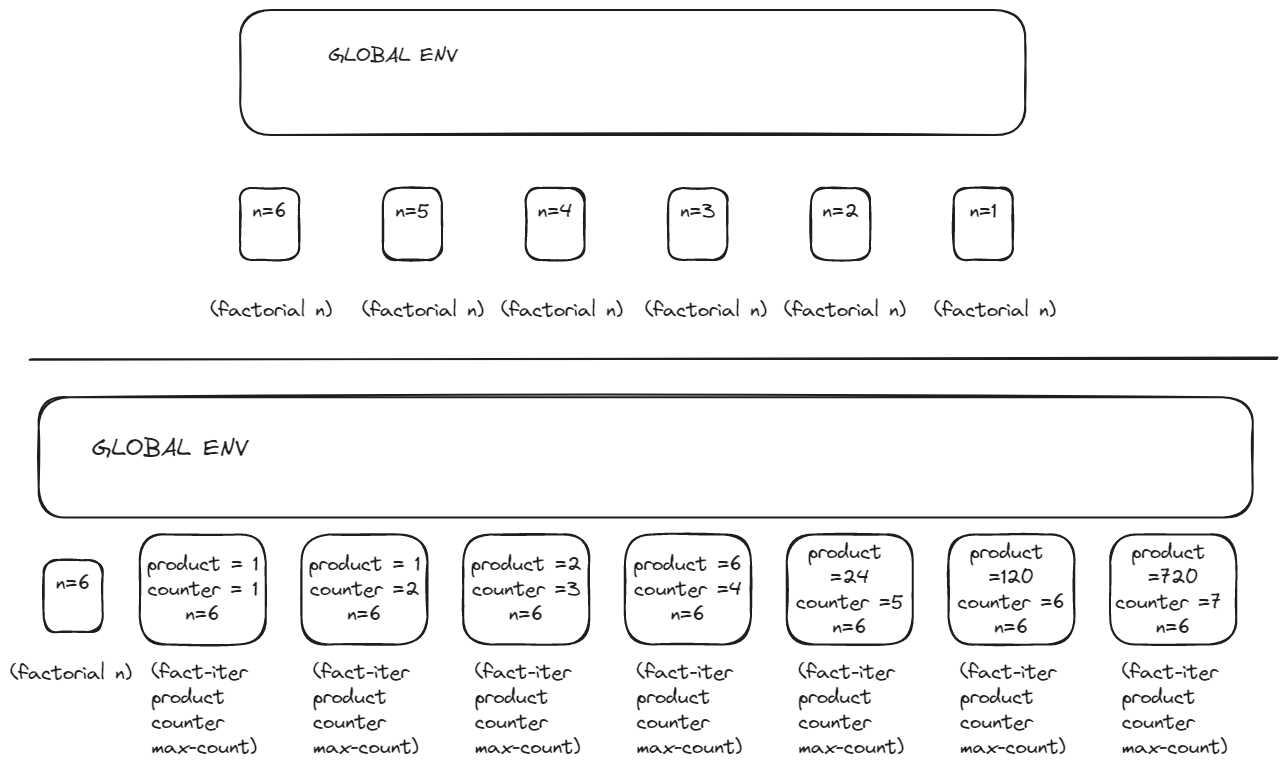
3.10
I guess…
There is an unused env which stands for the ((lambda (balance) ⟨body⟩) 100)
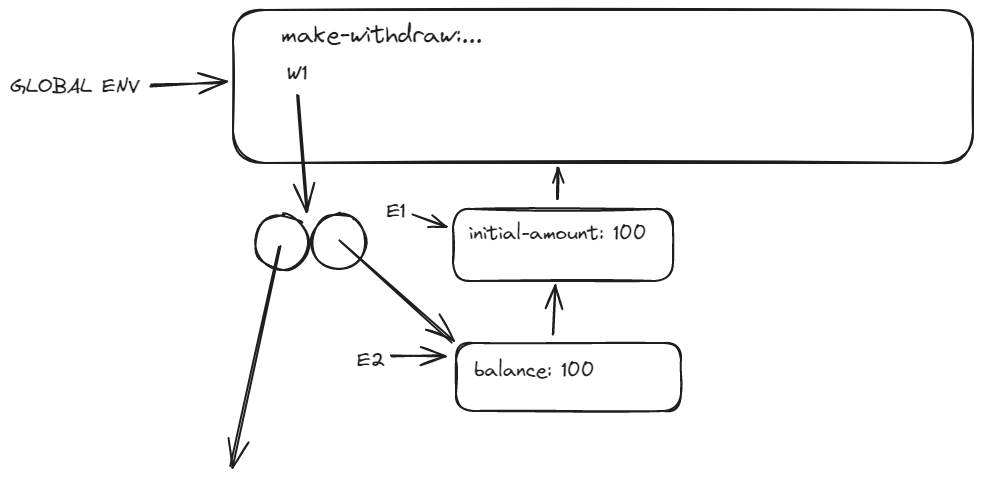
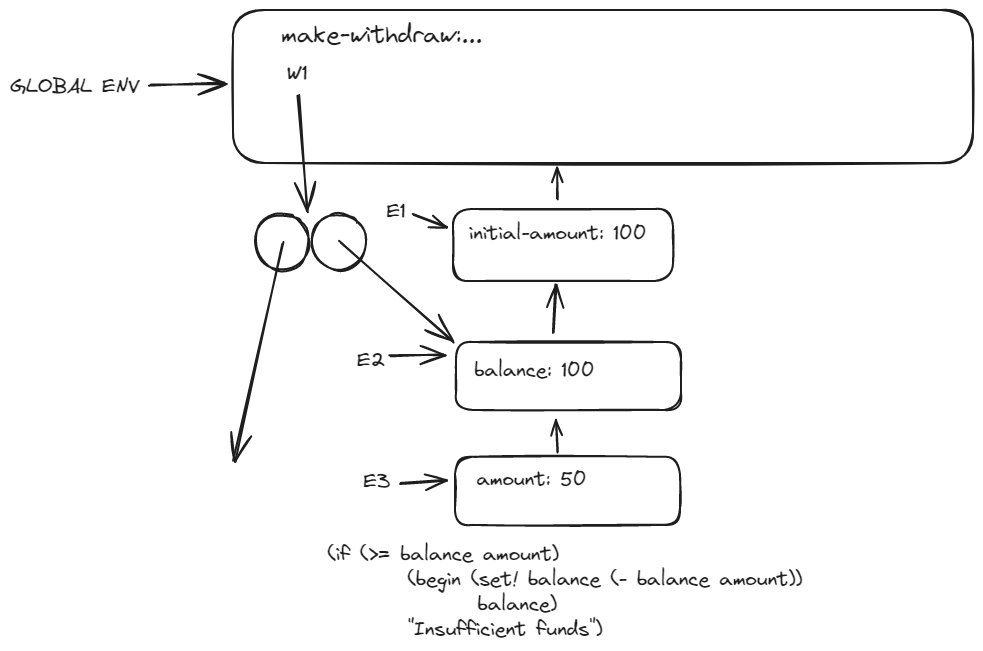
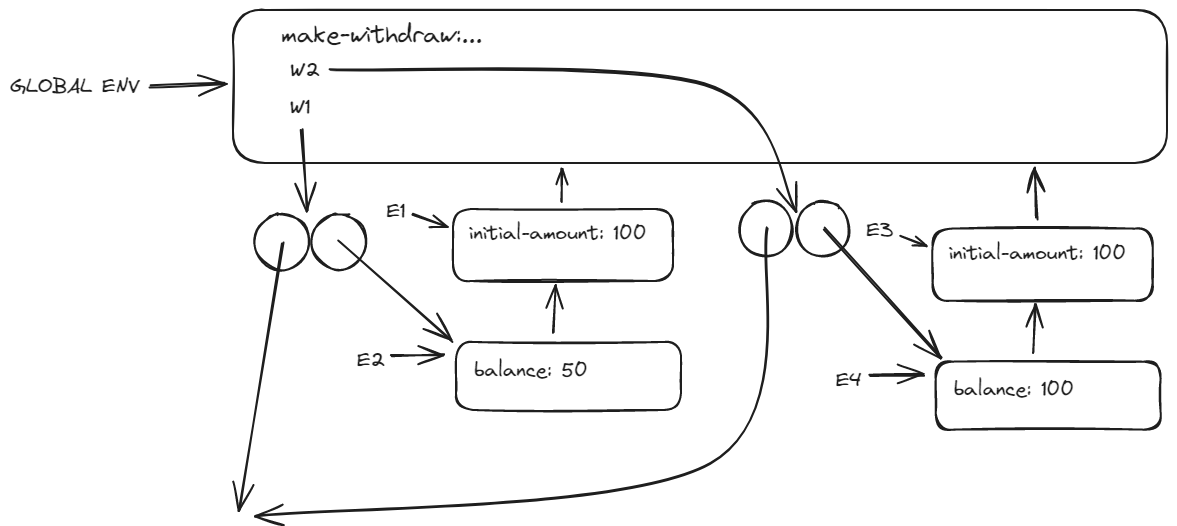
3.11
(define acc (make-account 50))
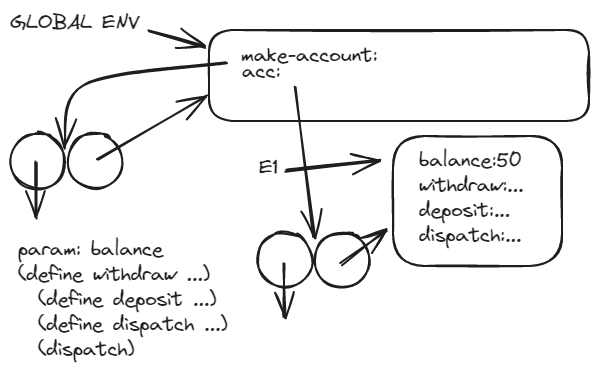
((acc 'deposit) 40)
I’m not sure how to express the another call (( ) ).
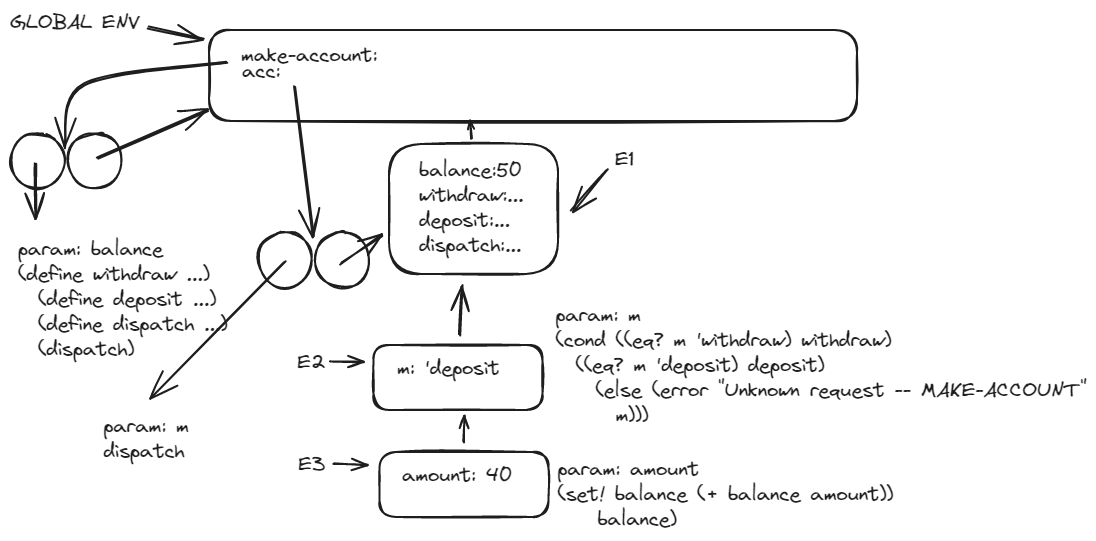
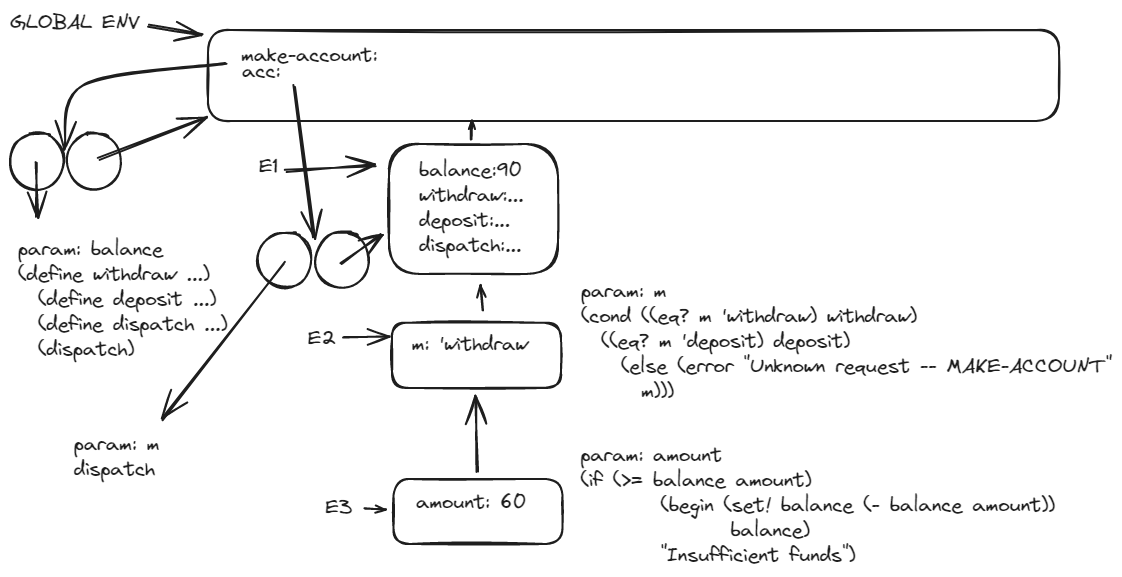
((acc 'deposit) 60)
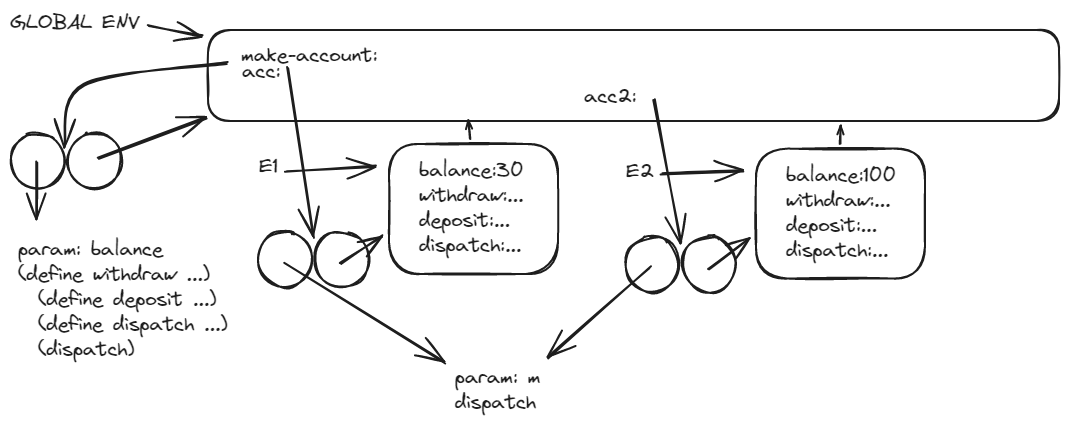
(define acc2 (make-account 100))
They only share the same dispatch code.
3.3
#! /bin/racket
#lang sicp
I see.
3.3.4 circuit? What’s wrong with you.
3.12
Drawings again.
Now we don’t have set-cdr!. Racket! OK, I just need to import them.
(require rnrs/mutable-pairs-6)
(require compatibility/mlist)
(define (mappend x y)
(if (null? x)
y
(mcons (mcar x) (append (mcdr x) y))))
(define (append! x y)
(set-cdr! (mlast-pair x) y)
x)
(define (mlast-pair x)
(if (null? (mcdr x)) x (mlast-pair (mcdr x))))
(define x (mlist 'a 'b)) (define y (mlist 'c 'd)) (define z (mappend x y)) z (mcons 'a (mcons 'b (mcons 'c (mcons 'd '())))) (mcdr x)
(b)
(define w (append! x y)) w (mcons 'a (mcons 'b (mcons 'c (mcons 'd '())))) (mcdr x)
(b c d)
I don’t want to draw. This problem illustrate the difference between pointer and value manipulation. append creates a new list and append! change the original list.
3.13
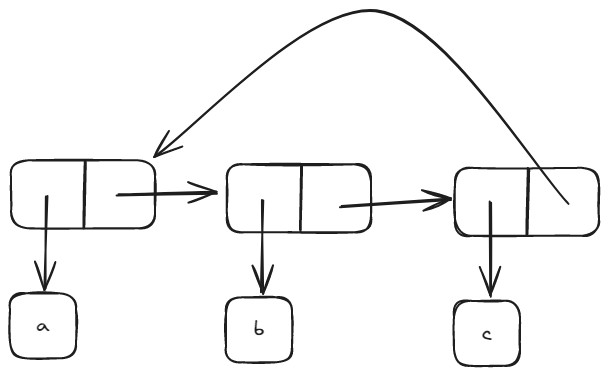
What happens if we try to compute (last-pair z)?
Infinite loop.
3.14
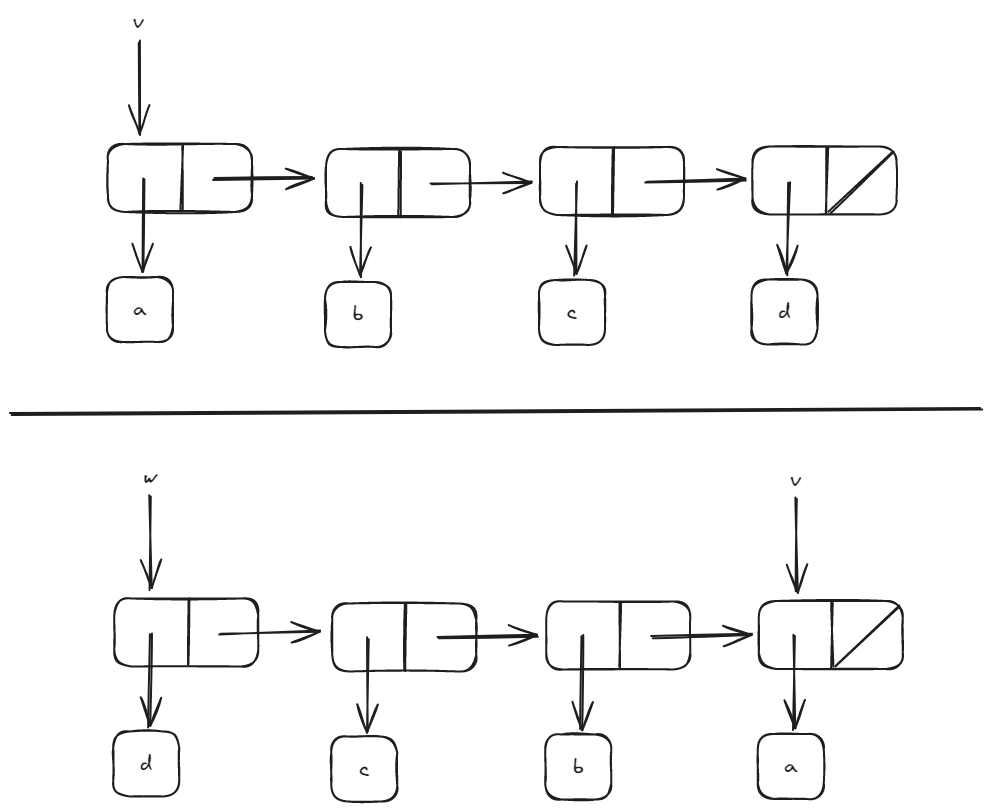
It seems the mystery reverse the order of the given list. Besides, it consumes no extra memory space and the order of growth is O(n).
(a b c d)
(d c b a)
(a)
3.15
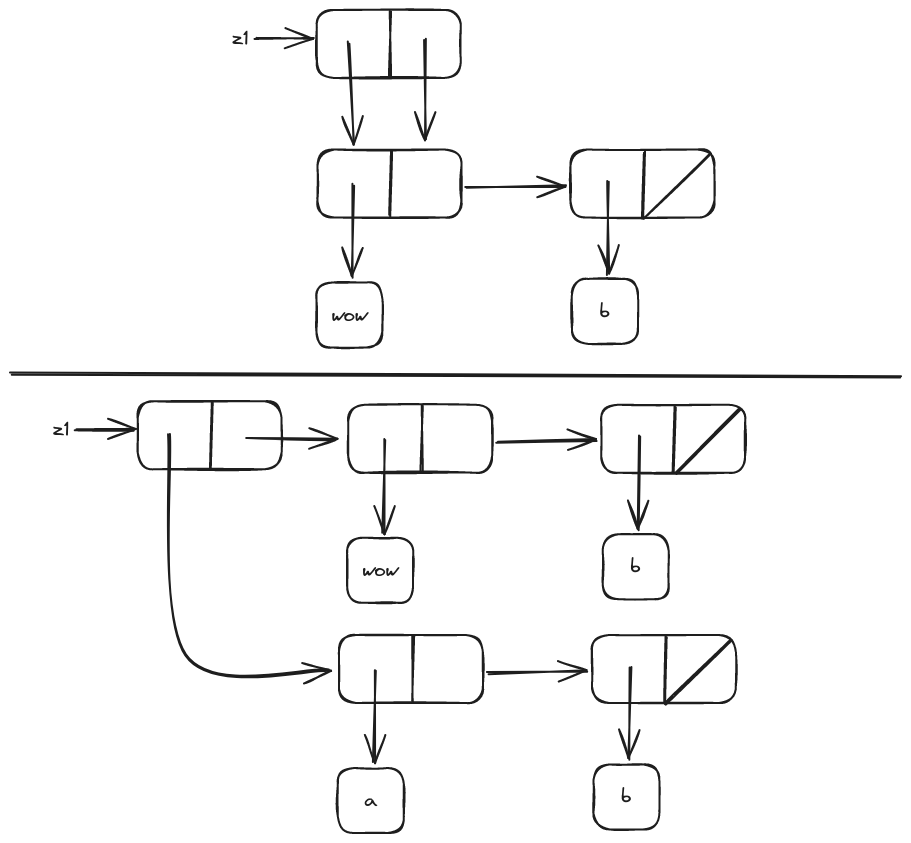
These are the effects of pointers. z1 has the two pointers point to the same pair so the set-to-wow! seemingly change the both part of the pair.
3.16
made up of exactly three pairs
Does that mean three cons?
> (count-pairs (cons 3 (cons 2 (cons 1 null))))
3
> (define a (cons 2 '(1)))
> a
'(2 1)
> (define b (cons a (cdr a)))
> b
'((2 1) 1)
> (count-pairs b)
4
> (define a (cons 1 null))
> (define b (cons a a))
> (define c (cons b b))
> a
'(1)
> b
'((1) 1)
> c
'(((1) 1) (1) 1)
> (count-pairs c)
7
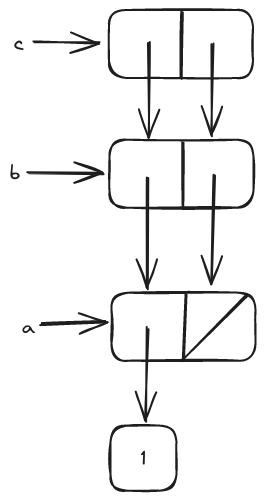
3.17
We need to use the eq? to remove calculated pairs.
(define (count-pairs x)
(define counted null)
(define (aux n)
(if (or (not (pair? n)) (memq n counted))
0
(begin
(set! counted (cons n counted))
(+ (aux (car n))
(aux (cdr n))
1))
)
)
(aux x)
)
I wonder whether this would calculate different pairs with the same value.
> a
'(3)
> (define b (cons a a))
> (eq? (car b) (cdr b))
#t
> (eq? a '(3))
#f> (memq '(3) (cons (car b) null))
#f
> (cons (car b) null)
'((3))
> (memq (car b) (cons (car b) null))
'((3))
> (memq '(3) (cons (car b) null))
#f
> (cons (car b) null)
'((3))
> (memq (car b) (cons (car b) null))
'((3))
Never mind. eq? only checks the pointer.
3.18
Typical.
(define (loop? x)
(define (aux a b)
(cond
((eq? a b) #t)
((null? (cdr b) #t))
((null? (cdr (cdr b)) #t))
(else (aux (cdr a) (cdr (cdr b)) ))
)
)
(aux x x)
)
3.19
As above.
3.20
It’s not a pair any more, but a procedure.
(define (cons x y)
(define (set-x! v) (set! x v))
(define (set-y! v) (set! y v))
(define (dispatch m)
(cond ((eq? m 'car) x)
((eq? m 'cdr) y)
((eq? m 'set-car!) set-x!)
((eq? m 'set-cdr!) set-y!)
(else (error "Undefined
operation: CONS" m))))
dispatch)
(define (car z) (z 'car))
(define (cdr z) (z 'cdr))
(define (set-car! z new-value)
((z 'set-car!) new-value)
z)
(define (set-cdr! z new-value)
((z 'set-cdr!) new-value)
z)
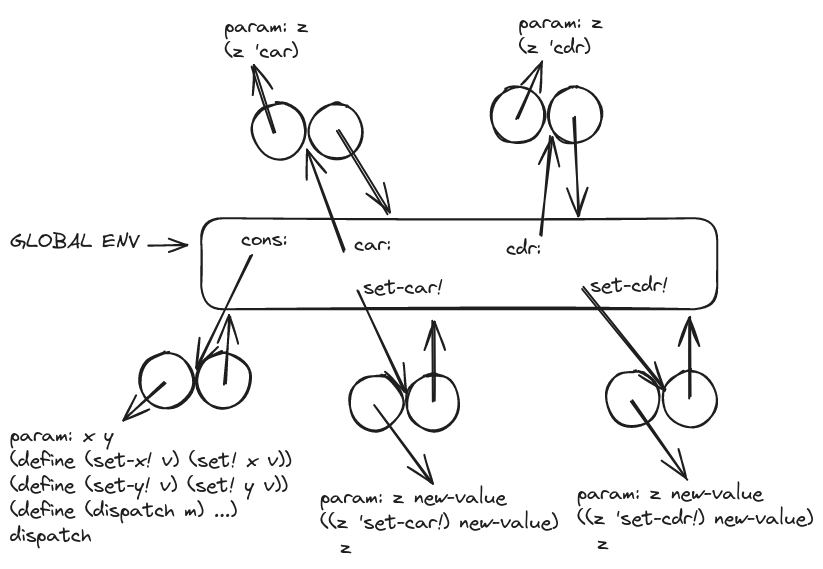
(define x (cons 1 2))
(define z (cons x x))
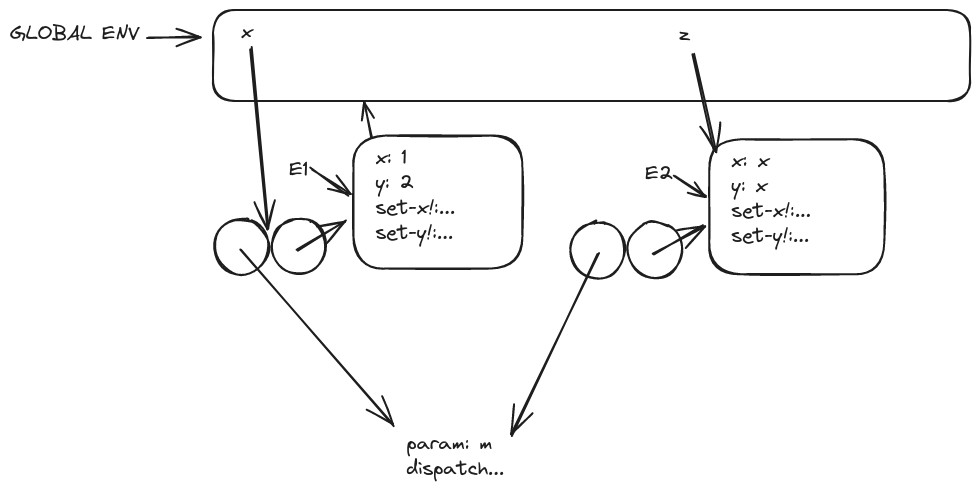
(set-car! (cdr z) 17)

Gross. I still don’t know how to express (() ).
3.21
(define (print-queue queue)
(mcar queue)
)
The interpreter print the queue’s front-ptr and rear-ptr at the same time. So it seems the element get inserted twice. Whether the queue is empty depends on the front-ptr which is relevant to the concrete implementation of delete-queue! and empty-queue?. I wonder this could really disturb the garbage collector.
3.22
(define (make-queue)
(let ((front-ptr null )
(rear-ptr null ))
(define (empty-queue? queue)
(null? (front-ptr queue)))
(define (set-front-ptr! queue item)
(set! front-ptr item))
(define (set-rear-ptr! queue item)
(set! rear-ptr item))
(define (insert-queue! queue item)
(let ((new-pair (mcons item '())))
(cond
((empty-queue? queue)
(set-front-ptr! queue new-pair)
(set-rear-ptr! queue new-pair)
queue)
(else
(set-mcdr! (rear-ptr queue) new-pair)
(set-rear-ptr! queue new-pair)
queue)
)))
(define (delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else (set-front-ptr! queue (mcdr (front-ptr queue)))
queue)))
(define (dispatch m)
(cond ((eq? m 'empty-queue?) empty-queue?)
((eq? m 'front-ptr) front-ptr)
((eq? m 'rear-ptr) rear-ptr)
((eq? m 'set-front-ptr!) set-front-ptr!)
((eq? m 'set-rear-ptr!) set-rear-ptr!)
((eq? m 'insert-queue!) insert-queue!)
((eq? m 'delete-queue!) delete-queue!)
(else
(error "Undefined operation: CONS" m))))
dispatch))
3.23
I made a double pointer element to represent the deque.
Maybe I’d write some selectors for the element itself. It’s confusing using mcar and mcdr now.
((element front-end) rear-end)
(define (make-deque) (mcons '() '()))
(define (empty-deque? deque)
(null? (front-ptr deque)))
(define (front-ptr deque) (mcar deque))
(define (rear-ptr deque) (mcdr deque))
(define (set-front-ptr! deque item)
(set-mcar! deque item))
(define (set-rear-ptr! deque item)
(set-mcdr! deque item))
(define (front-deque deque)
(if (empty-deque? deque)
(error "FRONT called with an empty deque" deque)
(mcar (front-ptr deque))))
(define (rear-deque deque)
(if (empty-deque? deque)
(error "FRONT called with an empty deque" deque)
(mcar (rear-ptr deque))))
(define (front-insert-deque! deque item)
(let ((new-pair (mcons (mcons item '()) '()) ))
(cond ((empty-deque? deque)
(set-front-ptr! deque new-pair)
(set-rear-ptr! deque new-pair)
deque)
(else
(set-mcdr! new-pair (front-ptr deque))
(set-mcdr! (mcar (front-ptr deque)) new-pair)
(set-front-ptr! deque new-pair)
deque))))
(define (rear-insert-deque! deque item)
(let ((new-pair (mcons (mcons item '()) '()) ))
(cond ((empty-deque? deque)
(set-front-ptr! deque new-pair)
(set-rear-ptr! deque new-pair)
deque)
(else
(set-mcdr! (rear-ptr deque) new-pair)
(set-mcdr! (mcar new-pair) (rear-ptr-deque))
(set-rear-ptr! deque new-pair)
deque))))
(define (front-delete-deque! deque)
(cond ((empty-deque? deque)
(error "DELETE! called with an empty deque" deque))
(else
(set-front-ptr! deque (mcdr (front-ptr deque)))
(set-mcdr! (mcar (front-ptr deque)) '())
deque)))
(define (rear-delete-deque! deque)
(cond ((empty-deque? deque)
(error "DELETE! called with an empty deque" deque))
(else
(set-rear-ptr! deque (mcdr (mcar (rear-ptr deque))))
(set-mcdr! (rear-ptr deque) '())
deque)))
3.24
we just need to rewrite assoc, all the inner methods use assoc to locate the key.
(define (make-table same-key?)
(define (assoc key records)
(cond ((null? records) false)
((same-key? key (caar records))
(car records))
(else (assoc key (cdr records)))))
.......
)
3.25
Sure enough you come.
(define (make-table)
(list '*table*))
(define (assoc key records)
(cond ((null? records) false)
((equal? key (caar records))
(car records))
(else (assoc key (cdr records)))))
(define (lookup keys table)
(define (find-final keys-left table-now)
(let ((record (assoc (car keys-left) (cdr table-now) )))
(if record
(if (null? (cdr keys-left))
(cdr record)
(find-final (cdr keys-left) record)
)
false))
)
(find-final keys table)
)
(define (insert! keys value table)
(define (aux remain-keys table-now)
(let ((record (assoc (car remain-keys) (cdr table-now))))
(if record
(if (null? (cdr remain-keys))
(set-cdr! record value)
(aux (cdr remain-keys) record)
)
(begin
(set-cdr! table-now (cons (cons (car remain-keys) '()) (cdr table-now) ) )
(aux remain-keys table-now)
)
)
'ok
)
)
(aux keys table)
)
3.26
Describe
Great.
cdr table is the records in the previous implemented table, now it is replaced with a tree. We could lookup the key by compare it with the entry key to decide which sub-tree to follow until we find or not find it in the final leaf.
Also, we may just modify the assoc and insert! so we could run the new implementation.
3.27
Plz, no more drawings.
(define memo-fib...) (define (memoize f)...)
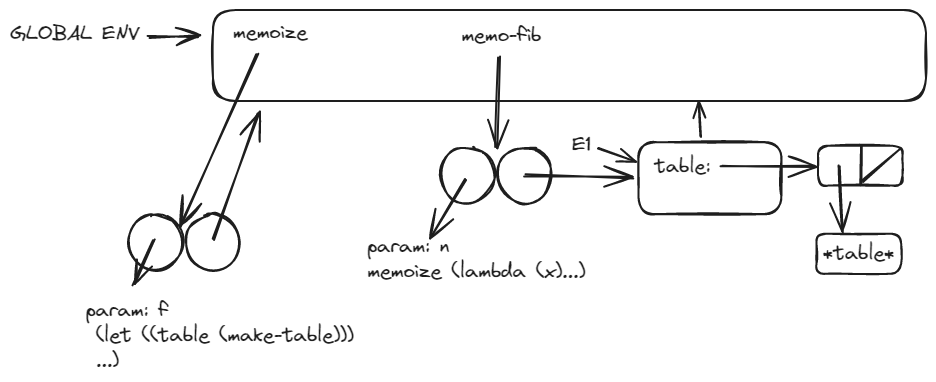
(memo-fib 3)-> (f 3) -> (+ (memo-fib 2) (memo-fib 1) ->
(+ (+ (memo-fib 2) (memo-fib 1)) (memo-fib 1) ->
(+ (+ (+ (memo-fib 1) (memo-fib 0)) (memo-fib 1)) (memo-fib 1)
So, the first element inserted in the table is 1.
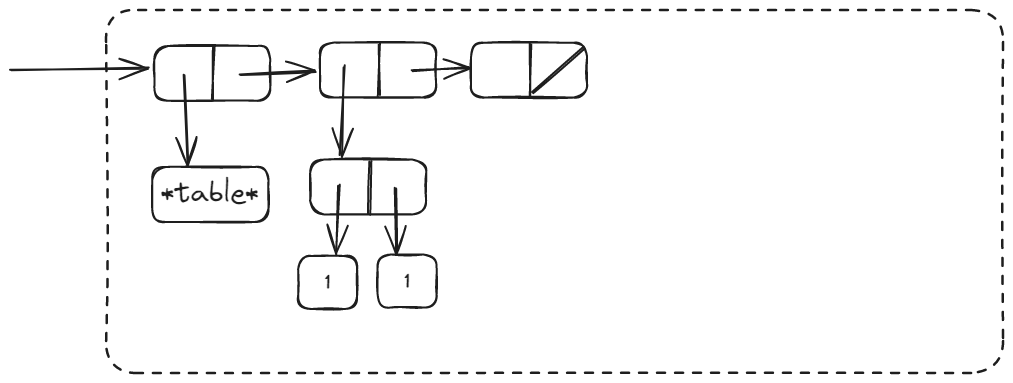
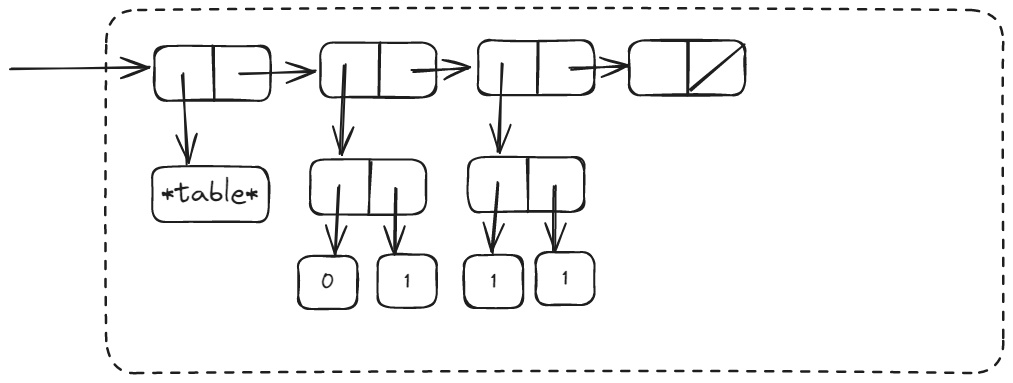
Then, the result of (memo-fib 2) will be inserted in table.
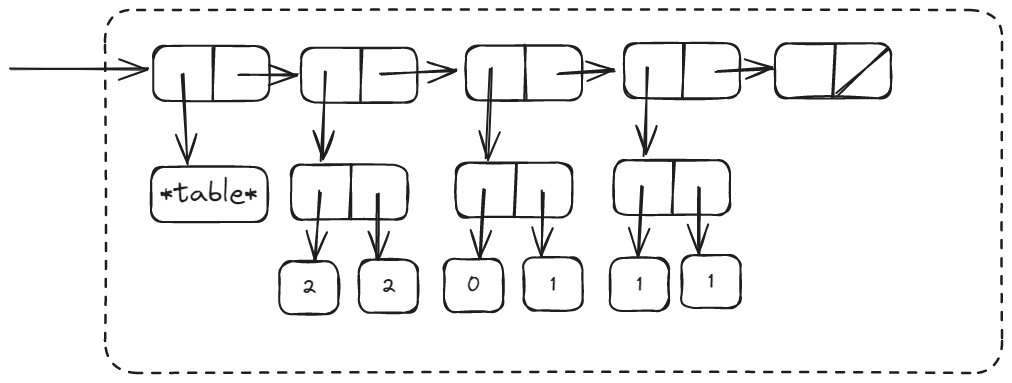
Finally, the result of (memo-fib 3).
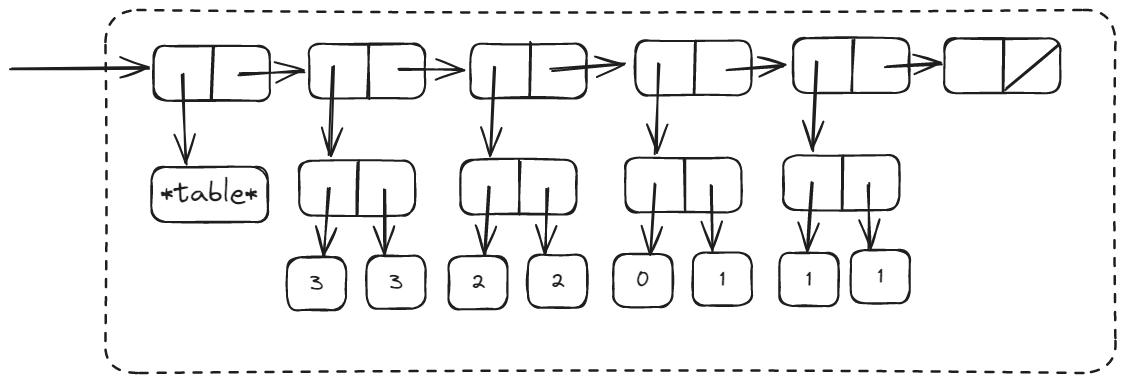
Explain why memo-fib computes thenth Fibonacci number in a number of steps proportional to n.
Because of the table, the (memo-fib n) for any n would be only calculated once. In the old fib, it cost much to recalculated.
3.28
S will become 1 whenever precisely one of A and B is 1, and C will become 1 whenever A and B are both 1.
It seems every signal will trigger the circuit once. What would happen if there’s only one signal?
(define (or-gate a1 a2 output)
(define (or-action-procedure)
(let ((new-value
(logical-or (get-signal a1) (get-signal a2))))
(after-delay
or-gate-delay
(lambda () (set-signal! output new-value)))))
(add-action! a1 or-action-procedure)
(add-action! a2 or-action-procedure)
'ok)
3.29
(define (or-gate a1 a2 output)
(let ((a11 (make-wire)) (a21 (make-wire)) (b (make-wire)))
(begin
(inverter a1 a11)
(inverter a a21)
(and-gate a11 a21 b)
(inverter b output)
)
)
)
It takes (+ (* 3 inverter-delay) and-gate-delay) time.
3.30
(define (ripple-carryadder al bl sl c)
(define (single-adder a-remain b-remain s-remain c-in)
(if (null? a-remain)
(set-signal! c (get-signal c-in))
(let ((c-next (make c-next)))
(begin
(full-adder (car a-remain) (car b-remain) c-in (car sl) c-next)
(signle-adder (cdr a-remain) (cdr b-remain) (cdr s-remain) c-next)
)
)
)
)
(let ((first-c (make-wire)))
(begin
(set-signal! first-c 0)
(signle-adder al bl sl first-c)
)
)
)
I’m not sure how does the parallel circuit works. I simply add all of them.
It takes n * full-adder delay, i.e. 2n * half-adder + n * or , i.e. 4n * and + 3n * or + 2n * invert.
3.31
If the procedure is not immediately run, the initial wire value 0 won’t be processed when the propagate is called. The result wire would always be the initial value 0 if the input wire is not set to another value, e.g. inverter input output. The output should be 1 when input is initially set as 0.
However, the processor is still registered in the wire action-procedures successfully, which means the following signal could be aware.
trace through the half-adder example
I guess the first sum 0 New-value = 0 won’t print?
3.32
Explain why this order must be used
Why, in my opinion, they are just different. They both have a intermediate state.
I know, if the procedures for each segment are not called in the order in which they were added to the agenda, then the intermediate segment would executed at last.
0,1 -> 1,1 (add-to-agenda! a1) -> 1,0 (add-to-agenda! a2)
If first in, first out, final state would be a2 i.e. output 0 , otherwise a1 i.e. output 1 which is incorrect.
3.33
(define (adder a b c)
(define (process-new-value)
(cond ((and (has-value? a) (has-value? b))
(set-value! c
(/ (+ (get-value a) (get-value b)) 2)
me))
((and (has-value? a) (has-value? c))
(set-value! b
(- (* 2 (get-value c)) (get-value a))
me))
((and (has-value? b) (has-value? sum))
(set-value! a
(- (* 2 (get-value c)) (get-value b))
me))))
(define (process-forget-value)
(forget-value! a me)
(forget-value! b me)
(forget-value! c me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- ADDER" request))))
(connect a me)
(connect b me)
(connect c me)
me)
3.34
Every parameter of the procedure should be the individual connector. In this case, the forget and set-value! rely on equal? to exclude the source connector and inform other connectors.
Also, when b is set to calculate a, both multiplier and multiplicand are a which has no value so it is not processed.
3.35
(define (squarer a b)
(define (process-new-value)
(if (has-value? b)
(if (< (get-value b) 0)
(error "square less than 0 -- SQUARER" (get-value b))
(set-value! a
(sqrt b)
me))
(if (has-value? a)
(set-value! b
(square a)
me)
'ignore
)))
(define (process-forget-value)
(forget-value! a me)
(forget-value! b me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- SQUARER" request))))
(connect a me)
(connect b me)
me)
3.36
They are not connected, right?
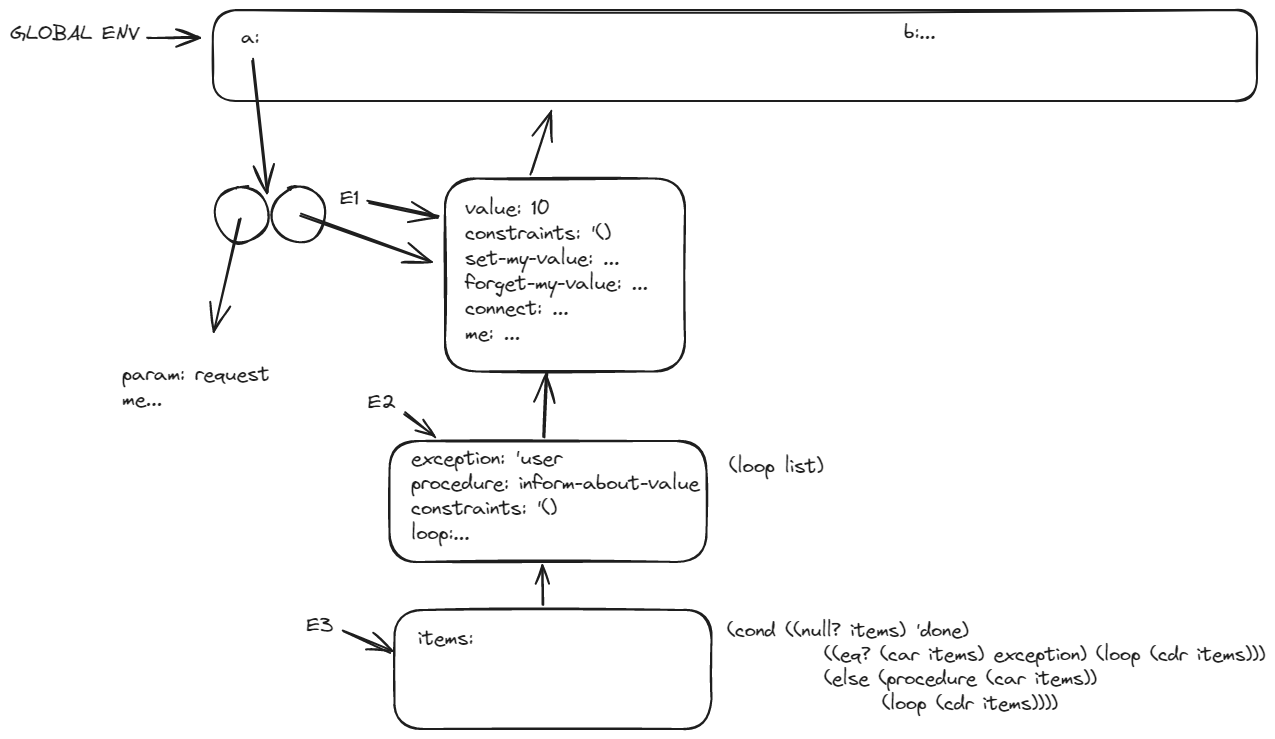
Please, no more drawing problems… This is not the whole picture, I ignored a big part of it.
3.37
(define (c- x y)
(let ((z (make-connector)))
(adder z y x)
z))
(define (c* x y)
(let ((z (make-connector)))
(multiplier x y z)
z))
(define (c/ x y)
(let ((z (make-connector)))
(multiplier z y x)
z))
(define (cv x)
(let ((z (make-connector)))
(constant x z)
z))
3.4
Great! Concurrency primitives for SICP for Racket 7
3.38
a.
Peter and Paul have the fixed amount.
Peter, Paul, Mary -> 45$
Peter, Mary, Paul -> 35$
Paul, Mary, Peter -> 50$
Mary, Paul, Peter -> 40$
b.
There are a bunch of possibilities.
More than these: 90$, 110$, 50$… Mary makes this more complicated. The book even demands drawings.
3.39
We don’t know the implementation of make-serializer. How could we make a conclusion? It could possibly make no changes.
I guess answers are these three.
101: P1 sets x to 100 and then P2 increments x to 101.
110: P2 changes x from 10 to 11 between the two times that P1 accesses the value of x during the evaluation of (* x x).
121: P2 increments x to 11 and then P1 sets x to x * x.
3.40
100 1000 1000000 10000 100000 total 5
1000000 only 1
3.41
I don’t agree. Reading a value is a one-step execution which can’t be interrupted.
Even if you protect it, someone still could modify the account balance after you check it. It’s just useless.
At least in this bank account scenario, there can’t be anything wrong. withdraw and deposit don’t set the balance to a intermediate state.
3.42
Does this actually protect the withdraw and deposit or does it just protect the produce of protected-withdraw and protected-deposit?
3.43
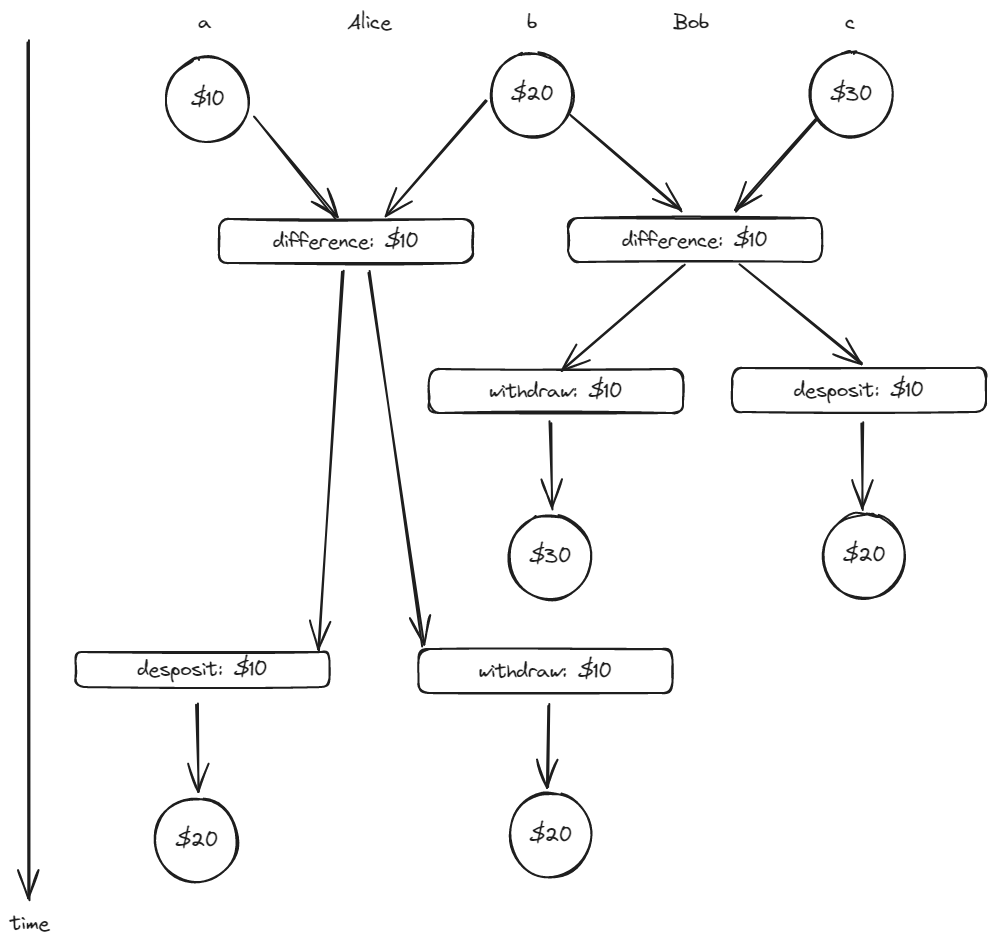
We still use the withdraw and deposit whose transaction is secured by the account inner serializer. So the sum of the balances in the accounts will be preserved.
3.44
exchange tries to make the two accounts exchange at last, while transfer just transfer and doesn’t guarantee anything but the transformation, and the account balance is secured by itself.
3.45
No no no, the withdraw and deposit use the same serializer as the exchange. So when exchange use it to prevent other exchange from influencing, it also prevent the withdraw and deposit truly reaching the balance.
So when it’s called, the program will keep wait till the world end.
3.46
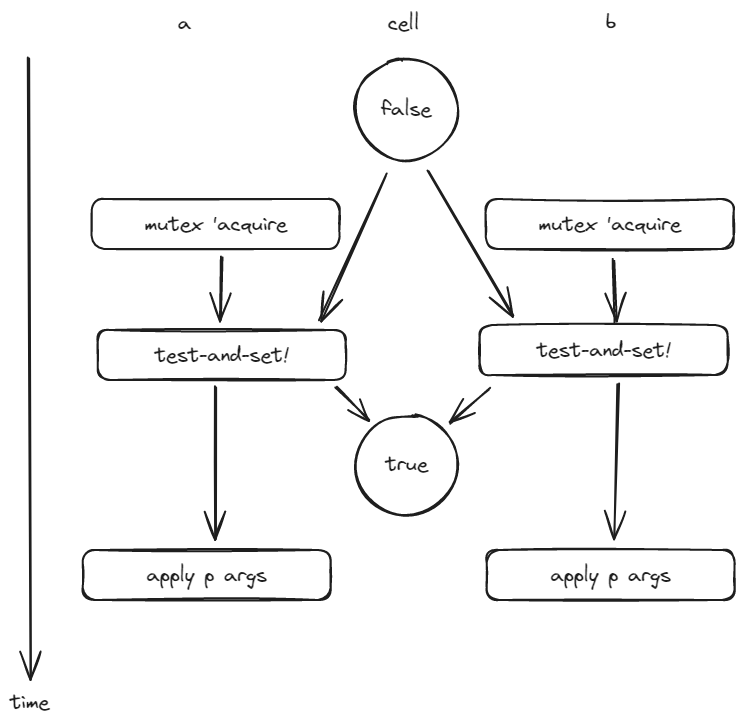
3.47
a.
We can lock the signals list.
(define (make-semaphore n)
(define (get-list m res)
(if (= m 0)
res
(get-list (- m 1) (cons false res))
)
)
(let ((signals (get-list)) (mutex (make-mutex)))
(define (try-until-acquire l)
(if (null? l
(try-next signals)
(if (test-and-set! (car l))
(try-next (cdr l))
)
))
)
(define (release-one l)
(if (null? l)
(release-one signals)
(if (not (test-and-set! (car l)))
(release-one (cdr l))
(clear! (car l))
)
)
)
(define (the-semaphore m)
(cond
((eq? m 'acquire)
(mutex 'acquire)
(try-until-acquire signals)) ; retry
(mutex 'release)
((eq? m 'release)
(mutex 'acquire)
(release-one! signals)
(mutex 'release))))
)
)
b.
Now we lock the every single cell in the list.
(define (make-semaphore n)
(define (get-list m res)
(if (= m 0)
res
(get-list (- m 1) (cons false res))
)
)
(let ((mutexs (get-list)))
(define (try-until-acquire l)
(if (null? l
(try-next mutexs)
(if (test-and-set! (car l))
(try-next (cdr l))
)
))
)
(define (release-one l)
(if (null? l)
(release-one mutexs)
(if (not (test-and-set! (car l)))
(release-one (cdr l))
(clear! (car l))
)
)
)
(define (the-semaphore m)
(cond
((eq? m 'acquire)
(try-until-acquire mutexs)) ; retry
((eq? m 'release) (release-one! mutexs))))
)
)
3.48
While Peter attempts to exchange a1 with a2 while Paul concurrently attempts to exchange a2 with a1, a1 has the smaller number so both of them need to acquire serialized procedure a1, one of them could succeed and the other would wait until the succeeded one finish his work. So the deadlock wouldn’t happen.
(define getnumber
(let ((first 0))
(begin
(set! first (+ 1 first))
first
)
)
)
(define (make-account-and-serializer balance)
(define (withdraw amount)
(if (>= balance amount)
(begin
(set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((balance-serializer
(list ((make-serializer) (getnumber)))))
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
((eq? m 'balance) balance)
((eq? m 'serializer)
balance-serializer)
(else (error "Unknown request:
MAKE-ACCOUNT"
m))))
dispatch))
(define (serialized-exchange account1 account2)
(let ((serializer1 (account1 'serializer))
(serializer2 (account2 'serializer)))
(if (< (car serializer1) (car serializer2))
((serializer1 (serializer2 exchange))
account1
account2)
((serializer2 (serializer1 exchange))
account1
account2)
)
))
balance-serializer becomes a list which contains a number to notify its order.
serialized-exchange would relay on the number to determine the order to exchange.
3.49
There are a list of accounts, we need to withdraw 2$ from two of them which are available.
Alice gets account a serializer and wait for the account b while Bob gets the account b serializer and wait for the account a.
In this scenario, we can’t avoid deadlock.
3.5
Is the infinite stream somehow like a stack? So would all tail recursive procedures be rewritten in this form?
Man! Streams are so tough.
3.50
(define (stream-map proc . argstreams)
(if (stream-null? (car argstreams))
the-empty-stream
(cons-stream
(apply proc (map stream-car argstreams))
(apply stream-map
(cons proc
(map stream-cdr
argstreams))))))
3.51
> (define x
(stream-map
show
(stream-enumerate-interval 0 10)))
012345678910
> (stream-ref x 5)
5
> (stream-ref x 7)
7
Something wrong…s
I guess all the Racket guys got the same problem: sicp-ex-3.51 We don’t have the original delay function which would stop the parameter from executing before pass it to the procedure.
Yeah, Racket 模拟SICP的流(延时计算). It works for me.
Now it becomes:
○ → ./test.scm
0
1
2
3
4
55
6
77
There are two 5 and two 7, one is printed by the show, the other is the result of stream-ref.
I find it must be called like cons a (delay b) for the delay to work. When the parameter is passed into the procedure, it has been evaluated. So the macro in the blog made the new syntax to replace the cons-stream with the direct call to delay, because the delay can’t work inside the cons-stream procedure. So, it surly works.
3.52
(define seq
(stream-map
accum
(stream-enumerate-interval 1 20)))
(display-line sum)
(define y (stream-filter even? seq))
(display-line sum)
(define z
(stream-filter
(lambda (x)
(= (remainder x 5) 0)) seq))
(display-line sum)
(newline)
(stream-ref y 7)
○ → ./3.52
1
6
10
136
136
10
15
45
55
105
120
190
210'done
210
The memo makes the first several elements of the seq won’t be calculated again.
If the stream-cons is not memorized, the sum will always be the final printed stream or stream-ref value.
If it’s memorized, things will become more complicated.
So we only know about the seq has the first element as 1, the following elements will depend on the sum in the global env at that moment, every time we call it, it returns different values.
I’m still confused, it’s way too complicated. SICP! why don’t you have a standard answer?
See this sicp-ex-3.52 for more.
3.53
2^(n-1)
3.54
(define (mul-streams s1 s2)
(stream-map * s1 s2))
(define factorials
(cons-stream 1 (mul-streams integers factorials)))
3.55
(define (partial-sums s)
(cons-stream (stream-car s) (add-streams (stream-cdr s) (partial-sums s)))
)
It’s easy to crash into infinite loop while ref oneself. Take care.
3.56
(define S (cons-stream 1 (merge (merge (scale-stream S 2) (scale-stream S 3)) (scale-stream S 5) )))
3.57
I mean, it’s like what we have been talking about in chapter1. Some small numbers are being evaluated over and over again, which cost a lot.
3.58
(define S (expand 1 7 10))
(stream-ref S 0)
(stream-ref S 1)
(stream-ref S 2)
(stream-ref S 3)
○ → ./3.58.scm
1
4
2
8
(define S (expand 3 8 10))
(stream-ref S 0)
(stream-ref S 1)
(stream-ref S 2)
(stream-ref S 3)
○ → ./3.58.scm
3
7
5
0
The result is the exact result of (/ (* num radix) den). The first element is the integer part, followed by the decimal part.
3.59
1.
(define (integrate-series s)
(mul-streams s (div-streams (ones) (integers)))
)
2.
I guess…
(define cosine-series
(cons-stream 1 (scale-stream (integrate-series sine-series) -1)))
(define sine-series
(cons-stream 0 (integrate-series cosine-series)))
3.60
(define (mul-series s1 s2)
(cons-stream (* (stream-car s1) (stream-car s2))
(add-streams
(add-streams (scale-stream s2 (stream-car s1)) (scale-stream s1 (stream-car s2)))
(cons-stream 0
(mul-series (stream-cdr s1) (stream-cdr s2))) )))
(a1+b1+c1+d1+....) * (a2+b2+c2+d2+...) =(cons (a1*a2) (( a1 * (a2+b2+c2+...) + a2 * (a1+b1+c1+...) ) + (0 + (b1+c1+d1+...)*(b2+c2+d2+...) ), a1*a2 is the lowest coefficient, the following polys are the rest coefficients.
3.61
How could you…
I’m not sure whether this would incur infinite loop… I haven’t define the first element of X.
(define (invert-unit-series s)
(scale-stream (mul-series s (invert-unit-series s)))
)
Sure it does. I haven’t distinguished the S with SR.
Here is another answer from the sicp-ex-3.61. Thanks leafac.
(define (invert-unit-series series) (define inverted-unit-series (cons-stream 1 (scale-stream (mul-streams (stream-cdr series) inverted-unit-series) -1))) inverted-unit-series)
3.62
a / b = 1/a * b? Like this?
(define (div-series nums dems)
(let ((c (stream-car dems)))
(if (= c 0)
(error "wrong")
(mul-series nums
(invert-series dems))
)))
OK. Things are different for coefficients.
(define (div-series s1 s2) (let ((c (stream-car s2))) (if (= c 0) (error "constant term of s2 can't be 0!") (scale-stream (mul-series s1 (invert-unit-series (scale-stream s2 (/ 1 c)))) (/ 1 c)))))
3.63
Using the memo-proc won’t change these two versions’ procedures in efficiency. They are different in mechanism. memo only works on the same procedure!
Reasoner’s version works like this: every element calls n-1 times sqrt-improve.
(1.0 (sqrt-improve 1.0) (sqrt-improve (sqrt-improve 1.0)) (sqrt-improve (sqrt-improve (sqrt-improve 1.0))) ...)
While original version works like this: every element calls sqrt-improve with the last element. Name the streams as s0 s1 s2 s3....
(1.0 (sqrt-improve 1.0) (sqrt-improve s1) (sqrt-improve s2) ...)
3.64
(define (stream-limit stream tolerance)
(if (< (abs (- (stream-ref stream 1) (stream-ref stream 0)))
tolerance)
(stream-ref stream 1)
(stream-limit (stream-cdr stream) tolerance)))
3.65
I don’t know how rapidly do these sequences converge, I haven’t run them yet.
(define (ln-summands n)
(cons-stream
(/ 1.0 n)
(stream-map - (ln-summands (+ n 1)))))
(define ln-stream
(partial-sums (ln-summands 1)) 4)
3.66
interleave makes the result stream are selected alternatively from two pieces (S0, T1) (S0, T2)... and (S1, T1) (S1, T2).... So before the 100th element (1, 100) in the second piece, there are 1 (part one) + 98 (part two) + 97 (part three) (part two is counted first in interleave, so part three is 97) = 198.
In the part two, half the steps are in the part one, so it must *2 in the final result. So in the nth line, the main body of the formula should be something like 2^n * …
So now we need to determine the diagonal elements. I find a pic in Scheme wiki.
1 2 3 4 5 6 7 8 9 ... 100 1 1 2 4 6 8 10 12 14 16 198 2 3 5 9 13 17 21 25 29 3 7 11 19 27 35 43 51 4 15 23 39 ..... 5 31 ......... . . 100 ------------------------------------- (2^100 - 1)
The half of all is in the first line, the half of the other half is in the second line… So, let’s count reversely, the diagonal element (n, n) is 1 now, then the n-1 line has taken double of it which is 2, the the n-2 line which is 4 as 2*2 … the first line is 2^ (n-1) as n-(n-1), so the (n,n) diagonal element has the order of 2^0 + 2^1 + … + 2^(n-1) = 2^n - 1.
Now suppose that the nth line is the first line and the diagonal element with the order of (2 ^ n -1) is the first number, the mth number in the line n should has the order of ( (2 ^ n -1) + m + (m-1)), but we don’t count the line above which will took the
No way. Let just observe the graph. You can see the regulation. At least I found out the diagonal element.
f(n,m) m>=n (m,n is Z+)
(m-n=0): 2^n - 1
(m-n=1): (2^n - 1) + 2^(n - 1)
(m-n>1): (2^n - 1) + 2^(n - 1) + (m - n - 1) * 2^n
3.67
Like this? I divide the entire graph into four parts and we need to interleave in the interleave.
(define (all-pairs s t)
(cons-stream
(list (stream-car s) (stream-car t))
(interleave
(interleave
(stream-map (lambda (x)
(list (stream-car s) x))
(stream-cdr t))
(pairs (stream-cdr s) (stream-cdr t)))
(stream-map (lambda (x)
(list (stream-car t) x))
(stream-cdr s))
)
)
)
3.68
Most of the elements would be missing, I simulated in my mind and I guess there will only be the first row and the diagonal elements left.
3.69
It’s like two doubles, now I even can’t draw a graph. How to combine them?
Genius! Still the first element is s0=t0=u0, and the part two is s0 with the whole possibilities of t and ` u, followed by a recursive call of triples (cdr s) (cdr t) (cdr u)`. Now the whole graph is included.
(define (triples s t u)
(cons-stream
(list (stream-car s)
(stream-car t)
(stream-car u))
(interleave (stream-map (lambda (x) (cons (stream-car s) x))
(stream-cdr (pairs t u)))
(triples (stream-cdr s)
(stream-cdr t)
(stream-cdr u)))))
And then there is a easy filter.
(define (phythagorean-numbers)
(define (square x) (* x x))
(define numbers (triples integers integers integers))
(stream-filter (lambda (x)
(= (square (caddr x))
(+ (square (car x)) (square (cadr x)))))
numbers))
3.70
Now it’s finally completed. I’m looking forward to using such a weighted procedure. I’m confused about the interleave then.
Take care, if weight thinks both have the same weight, we wouldn’t abandon any of them.
(define (merge-weighted s1 s2 weight)
(cond ((stream-null? s1) s2)
((stream-null? s2) s1)
(else
(let ((s1car (stream-car s1))
(s2car (stream-car s2)))
(cond ((weight s1car s2car)
(cons-stream
s1car
(merge-weighted (stream-cdr s1)
s2 weight)))
((weight s2car s1car)
(cons-stream
s2car
(merge-weighted s1
(stream-cdr s2) weight)))
(else
(cons-stream
s1car
(merge-weighted
(stream-cdr s1)
s2
weight))))))))
(define (weighted-pairs s t weight)
(cons-stream
(list (stream-car s) (stream-car t))
(merge-weighted
(stream-map (lambda (x)
(list (stream-car s) x))
(stream-cdr t))
(weighted-pairs (stream-cdr s) (stream-cdr t) weight)
weight
)))
(define pos-orderby-sum
(weighted-pairs integers integers
(lambda (p1 p2)
(<
(+ (car p1) (cadr p1))
(+ (car p2) (cadr p2))
)
)
)
)
(define strange-stream (
(define raw (weighted-pairs integers integers
(lambda (p1 p2)
(<
(+ (* 2 (car p1)) (* 3 (cadr p1)) (* 5 (car p1) (cadr p1)))
(+ (* 2 (car p2)) (* 3 (cadr p2)) (* 5 (car p2) (cadr p2)))
)
)
))
(define (undivisible x)
(not (or
(= 0 (modulo x 2))
(= 0 (modulo x 3))
(= 0 (modulo x 5))
))
)
(stream-filter
undivisible
raw)
))
3.71
(define (tri x)
(* x x x)
)
(define (pair-tri-sum p1)
(+ (tri (car p1)) (tri (cadr p1)))
)
(define pos-orderby-tri-sum
(weighted-pairs integers integers
(lambda (p1 p2)
(<
(+ (tri (car p1)) (tri (cadr p1)))
(+ (tri (car p2)) (tri (cadr p2)))
)
)
)
)
(define (stream-equal stream)
(cond ((stream-null? stream)
the-empty-stream)
((= (pair-tri-sum (stream-ref stream 0)) (pair-tri-sum (stream-ref stream 1)))
(begin
(display-line (stream-ref stream 0))
(display-line (stream-ref stream 1))
(display-line (pair-tri-sum (stream-ref stream 0)))
(newline)
(cons-stream
(stream-car stream)
(stream-equal
(stream-cdr stream)))
)
)
(else (stream-equal
(stream-cdr stream)))))
(1 12)
(9 10)
1729
(1 12)
(2 16)
(9 15)
4104
(2 16)
(2 24)
(18 20)
13832
(2 24)
(10 27)
(19 24)
20683
(10 27)
(4 32)
(18 30)
32832
(4 32)
(2 34)
(15 33)
39312
'done
1729, 4104, 13832, 20683, 32832, 39312. Some irrelevant pairs are printed.
3.72
LOL, it’s stuck and got killed by OS. I must have done something infinite.
I modified them, remove the dirty display in the equal procedure. I’d say stream-square-equal is a bad name, actually it does the map job.
(define (square x)
(* x x)
)
(define (pair-square-sum p1)
(+ (square (car p1)) (square (cadr p1)))
)
(define (stream-square-equal stream)
(cond ((stream-null? stream)
the-empty-stream)
((and (= (pair-square-sum (stream-ref stream 0)) (pair-square-sum (stream-ref stream 1)))
(= (pair-square-sum (stream-ref stream 1)) (pair-square-sum (stream-ref stream 2)))
)
(cons-stream
(list (stream-ref stream 0) (stream-ref stream 1) (stream-ref stream 2) (pair-square-sum (stream-ref stream 0)))
(stream-square-equal
(stream-cdr stream)))
)
(else (stream-square-equal
(stream-cdr stream)))))
(define pos-orderby-square-sum
(weighted-pairs integers integers
(lambda (p1 p2)
(<
(pair-square-sum p1)
(pair-square-sum p2)
)
)
)
)
((1 18) (6 17) (10 15) 325)
((5 20) (8 19) (13 16) 425)
((5 25) (11 23) (17 19) 650)
((7 26) (10 25) (14 23) 725)
((2 29) (13 26) (19 22) 845)
'done
3.73
The figure looks complicated, but the problem is not that difficult.
(define (integral integrand initial-value dt)
(define int
(cons-stream
initial-value
(add-streams (scale-stream integrand dt)
int)))
int)
(define (RC r c dt)
(lambda (s v0)
(add-streams
(scale-stream s r)
(integral (scale-stream s (/ 1 c)) vo dt)
)
)
)
3.74
(define (zero-crossings sense-data)
(stream-map sign-change-detector
sense-data
(cons-stream 0 sense-data)))
3.75
The avpt is not of the average of last value and the current value, it’s the average of last average and the current value.
We need to add a last-avpt for the computation of current value of the result stream.
(define (make-zero-crossings
input-stream last-value last-avpt)
(let ((avpt
(/ (+ (stream-car input-stream)
last-value)
2)))
(cons-stream
(sign-change-detector avpt last-avpt)
(make-zero-crossings
(stream-cdr input-stream) (stream-car input-stream) avpt))))
3.76
Now there’s a critical question: where is the first element of smooth? I cons a 0 at the head of it as what the problem before did.
(define (make-zero-crossings input-stream smooth)
(define (aux smoothed-s)
(cons-stream
(sign-change-detector (stream-car smoothed-s) (stream-car (stream-cdr smoothed-s)))
(aux
(stream-cdr smoothed-s)))
)
(aux (cons-stream 0 (smooth input-stream)))
)
3.77
Nice idea, using delay to prevent circle denpendency.
(define (integral
delayed-integrand initial-value dt)
(cons-stream
initial-value
(let ((integrand
(force delayed-integrand)))
(if (stream-null? integrand)
the-empty-stream
(integral
(stream-cdr integrand)
(+ (* dt (stream-car integrand))
initial-value)
dt))
)
))
3.78
homogeneous second-order linear differential equation
Now this is the end. That’s enough. I’m done.
文档信息
- 本文作者:nyaaar
- 本文链接:https://nyaaarlathotep.github.io/2024/11/08/SICP-Exercise-3/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)