Chapter 2

The abstraction of data lead to the interface of the data.

Church numerals…

Each level is constructed by combining parts that are regarded as primitive at that level, and the parts constructed at each level are used as primitives at the next level. The language used at each level of a stratified design has primitives, means of combination, and means of abstraction appropriate to that level of detail.

Generic interface as dispatching on type.

One weakness is that the generic interface procedures (real-part, imag-part, magnitude, and angle) must know about all the different representations.
Another weakness of the technique is that even though the individual representations can be designed separately, we must guarantee that no two procedures in the entire system have the same name.
The issue underlying both of these weaknesses is that the technique for implementing generic interfaces is not additive.

message passing.

…instead of using “intelligent operations” that dispatch on data types, to work with “intelligent data objects” that dispatch on operation names.
One limitation of this organization is it permits only generic procedures of one argument.

Just like OO? Well, not that like.

The methods belonging in generic types, especially the Combining Data of Different Types. Do you have any idea?

Coercion? Implicit Type Conversion!

2.1

(define (make-rat n d)
 (let ((g (gcd n d)))
 (if (< (* n d) 0)
    (cons (- (abs (/ n g))) (abs (/ d g)))
    (cons (abs (/ n g)) (abs (/ d g)))
 )
 )
)

> (make-rat 2 -3)
'(-2 . 3)
> (make-rat 2 3)
'(2 . 3)
> (make-rat -2 3)
'(-2 . 3)
> (make-rat -2 -3)
'(2 . 3)

2.2

(define (print-point p)
 (display "(")
 (display (x-point p))
 (display ",")
 (display (y-point p))
 (display ")"))


(define (x-point p)
   (car p)
)
(define (y-point p)
   (cdr p)
)
(define (make-point x y)
   (cons x y)
)
(define (make-segment x y)
   (cons x y)
)
(define (start-segment s)
   (car s)
)
(define (end-segment s)
   (cdr s)
)

(define (midpoint-segment s)
   (make-point 
      (average (x-point (start-segment s)) (x-point (end-segment s)))
      (average (y-point (start-segment s)) (y-point (end-segment s)))
   )
)

2.3

Maybe add another layer for edge length?

(define (make-rectangle a b)
   (cons a b)
)
(define (edge-a s)
   (car s)
)
(define (edge-b s)
   (cdr s)
)
(define (point-length one two)
)

(define (side-length r)
   (let ((a (edge-a r)))
   (let ((b (edge-b r)))
   (cons
      (point-length (start-segment a) (end-segment a))
      (point-length (start-segment b) (end-segment b))
   )
   )
   )
)

(define (area r)
(let ((edge-lengths (side-length r)))
   (* (car edge-lengths) (cdr edge-lengths))
)
)

(define (perimeter r)
(let ((edge-lengths (side-length r)))
   (* 2 (+ (car edge-lengths) (cdr edge-lengths)))
)
)

2.4

 (define (cons x y)
 (lambda (m) (m x y)))
 (define (car z)
 (z (lambda (p q) p)))
 (define (cdr z)
 (z (lambda (p q) q)))

> (cons 1 2)
#<procedure>
> (car (cons 1 2))
1
> (cdr (cons 1 2))
2

2.5

I don’t get it, it just means some renames?

Ok.

(define (cons a b)
    (* (expt 2 a) (expt 3 b))
)

(define (car z)
    (if ( = (remainder z 2) 0)
        (+ 1 (car (/ z 2)))
        0
    )
)
(define (cdr z)
    (if ( = (remainder z 3) 0)
        (+ 1 (cdr (/ z 3)))
        0
    )
)

2.6

Wow… The num means applying how many f to x. So if you take zero and add as x and f, then the whole pack would be the real nums.

(define one
    (lambda (f)
        (lambda (x) (f x))
    )
)
(define two
    (lambda (f)
        (lambda (x) (f (f x)))
    )
)

Good news, a + b = b + a.

(define (plus a b)
    (lambda (f)
        (lambda (x)
            ((b f) ((a f) x))
        )
    )
)

Let me guess, what is the definition of multiply?

Well then. Instead of handling x, let’s handle f.

(define (multiply a b)
    (lambda (f)
        (lambda (x)
            ((b (a f)) x)
        )
    )
)

So, the function comes first than the num itself?

some test:

> ((two add1) 3)
5
> ((one add1) 3)
4
> (((plus one two) add1) 3)
6
> (((multiply two two) add1) 3)
7

2.7

(define (make-interval a b) (cons a b))

    (define (upper-bound c)
        (max (car c) (cdr c))
    )
    (define (lower-bound c)
        (min (car c) (cdr c))
    )

2.8

(define (sub-interval x y)
  (make-interval (- (upper-bound x) 
                    (lower-bound y))
                 (- (lower-bound x) 
                    (upper-bound y))))

2.9

Both addition and subtraction result in a interval of the sum of two intervals.

It’s obvious multiply and divide don’t have a proper function of interval for negative numbers.

2.10

How to signal a error in Scheme?

(define (div-interval x y)
  (if (or (<= 0 (upper-bound y)) (<= 0 (lower-bound y)))
  	(raise "some bound is zero")
    (mul-interval x 
                (make-interval 
                 (/ 1.0 (upper-bound y)) 
                 (/ 1.0 (lower-bound y))))
  )
)

(define (make-interval a b)
	(if (or (<= 0 (upper-bound y)) (<= 0 (lower-bound y)))
		(raise "some bound is zero")
		(cons a b)
	)
)

2.11

3*3 = 9 cases in which every case is different. Obviously, it need 4 multiply when two interval are both neg-pos.

Rewrite this procedure using Ben’s suggestion.

I copied, it’s quite annoying.

(define (mul-interval x y)
  (let ((low-x (lower-bound x))
        (low-y (lower-bound y))
        (up-x (upper-bound x))
        (up-y (upper-bound y)))
    (cond ((and (>= low-x 0) (>= up-x 0))
           (cond ((and (>= low-y 0) (>= up-y 0)) ; + + | + +
                  (make-interval (* low-x low-y)
                                 (* up-x up-y)))
                 ((and (<= low-y 0) (>= up-y 0)) ; + + | - +
                  (make-interval (* up-x low-y)
                                 (* up-x up-y)))
                 ((and (<= low-y 0) (<= up-y 0)) ; + + | - -
                  (make-interval (* up-x low-y)
                                 (* low-x up-y)))))
          ((and (<= low-x 0) (>= up-x 0))
           (cond ((and (>= low-y 0) (>= up-y 0)) ; - + | + +
                  (make-interval (* low-x up-y)
                                 (* up-x up-y)))
                 ((and (<= low-y 0) (>= up-y 0)) ; - + | - + 
                  (make-interval (min (* low-x up-y) (* up-x low-y))
                                 (max (* low-x low-y) (* up-x up-y))))
                 ((and (<= low-y 0) (<= up-y 0)) ; - + | - -
                  (make-interval (* up-x low-y)
                                 (* low-x low-y)))))
          ((and (<= low-x 0) (<= up-x 0))
           (cond ((and (>= low-y 0) (>= up-y 0)) ; - - | + +
                  (make-interval (* low-x up-y)
                                 (* up-x low-y)))
                 ((and (<= low-y 0) (>= up-y 0)) ; - - | - +
                  (make-interval (* low-x up-y)
                                 (* low-x low-y)))
                 ((and (<= low-y 0) (<= up-y 0)) ; - - | - -
                  (make-interval (* up-x up-y)
                                 (* low-x low-y))))))))

2.12

(define (make-center-percent c w)
  (make-interval (- c (* c w)) (+ c (* c w))))
  
(define (center i)
  (/ (+ (lower-bound i) 
        (upper-bound i)) 
     2))
     
(define (percent i)
	(/
		(- (upper-bound i) (center i)) 
	    (center i)
	)
)

2.13

Since the tolerance is small enough, I’d try to simplify the formula by ignoring part of the res.

The new multiply assuming all the numbers are positive:

(define (mul-interval x y)
    (make-interval (* (upper-bound x) (upper-bound y))
                   (* (lower-bound x) (lower-bound y))
)

which approximately equals to:

(define (mul-interval x y)
    (make-center-percent (* (center x) (center y))
                   (* (percent x) (percent y))
)

Lem is so blunt.

> (define r1 (make-interval 3 0.25))
> (define r2 (make-interval 5 0.1))
> (par1 r1 r2)
'(0.003125 . 42.85714285714286)
> (par2 r1 r2)
'(0.07142857142857142 . 1.875)

2.14

2.2

Finally, it comes to some familar topic.

In general, an operation for combining data objects satisfies the closure property if the results of combining things with that operation can themselves be combined using the same operation.

So, this is the true definition of closure. It’s about hierarchical.

2.17

(define (last-pair p)
	(define (aux p e)
		(if (null? p)
			e
			(aux (cdr p) (car p))
		)
	)
	(aux p null)
)

2.18

(define (reverse l)
	(define (aux remain r)
		(if (null? remain)
			r
			(aux (cdr remain) (cons (car remain) r))
		)
	)
	(aux l null)
)

2.19

(define (first-denomination c)
	(car c)
)

(define (except-first-denomination c)
	(cdr c)
)

(define no-more? null?)

The order of the list coin-values doesn’t affect the answer produced by cc.

Every possibility will be tested, no one would escape.

2.20

(define (same-parity f . l)
	(define (aux remain parity)
		(if (null? remain)
			null
			(if (= parity (modulo (car remain) 2))
			(cons (car remain) (aux (cdr remain) parity))
			(aux (cdr remain) parity)
		)
		)
	)
	(aux (cons f l) (modulo f 2))
)

2.21

 (define (square-list items)
 (if (null? items)
 nil
 (cons (square (car items)) (square-list (cdr items)))))

 (define (square-list items)
 (map queare items))

2.22

This is a classic problem of tail recursion with lists. In the first attempt, the last element is consed to the result first, so the result is reversed. In the second attempt, consing a list to an element does not create a normal list.

2.23

How to throw a useless return value of a function in Scheme? Or let the procedure continue to run.

(define (for-each f l)
    (
        (if (null? l)
            '()
            (cons (f (car l )) (for-each f (cdr l)))
        )
    )
)

I’d use begin.

(define (for-each p lst)
    (if (not (null? lst))
        (begin
            (p (car lst))
            (for-each p (cdr lst)))))

2.24

> (list
   1 (list 2 (list 3 4)))
'(1 (2 (3 4)))

How do I draw a tree?

2.24

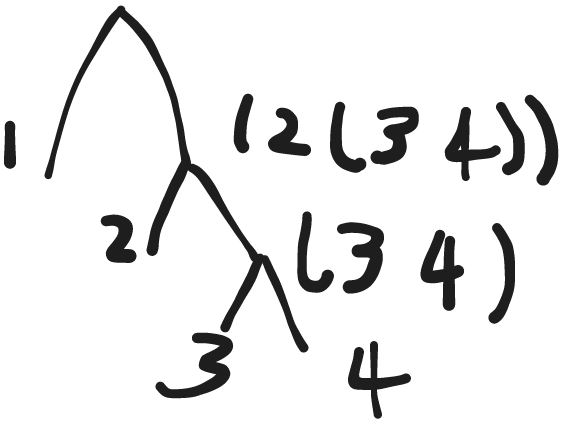
2.25

> (car (cdr (car (cdr (cdr '(1 3 (5 7) 9))))))
7
> (car (car '((7))))
7
> (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr '(1 (2 (3 (4 (5 (6 7))))))))))))))))))
7

Come on.

2.26

>  (append x y)
'(1 2 3 4 5 6)
>  (cons x y)
'((1 2 3) 4 5 6)
>  (list x y)
'((1 2 3) (4 5 6))

2.27

(define (deep-reverse l)
    (define (aux remain r)
        (cond 
            ((null? remain) r)
            ((pair? (car remain)) (aux (cdr remain) (cons (deep-reverse (car remain)) r)))
            (else (aux (cdr remain) (cons (car remain) r)))
        )
    )
    (aux l null)
)

2.28

(define (fringe t)
    (cond
        ((null? t) null)
        ((list? t) (append (fringe (car t)) (fringe (cdr t))))
        (else (list t))
    )
)

2.29

(define (left-branch  b)
    (car b)
)

(define (right-branch  b)
    (car (cdr b))
)

(define (branch-length b)
    (car b)
)

(define (branch-structure b)
    (car (cdr b))
)

(define (total-weight b)
    (define (weight s)
        (if (list? s)
            (total-weight s)
            s
        )
    )
    (+ (weight (left-branch b)) (weight (right-branch b)))
)

(and (balanced left) (balanced right) (equal torque))

(define (balanced b)
    (define (balanced-branch br)
        (if (list? (branch-structure br))
            (balanced (branch-structure))
            true
        )
    )
    (and
        (= (* (weight (left-branch b)) (branch-length (left-branch b))) (* (weight (right-branch b)) (branch-length (right-branch b))))
        (balanced-branch (left-branch b))
        (balanced-branch (right-branch b))
    )
)

A little. Maybe more than a little, cause the branch hanging prediction needs to be changed.

Anyway, list a b is cons a (list b)

2.30

(define (square-tree tree)
 (cond ((null? tree) null)
 ((not (pair? tree)) (* tree tree))
 (else (cons (square-tree (car tree))
 (square-tree (cdr tree))))))

(define (square-tree tree)
 (map (lambda (sub-tree)
 (if (pair? sub-tree)
 (square-tree sub-tree)
 (* sub-tree sub-tree)))
 tree))

2.31

(define (tree-map f tree)
    (map 
    (lambda (sub-tree)
    (if (pair? sub-tree)
    (tree-map f sub-tree)
    (f sub-tree))) 
    tree)
)

2.32

 (define (subsets s)
 (if (null? s)
 null
 (let ((rest (subsets (cdr s))))
 (append rest (map (lambda (poss) (cons (car s) poss)) rest)))))

2.33

(define (accumulate op initial sequence)
 (if (null? sequence)
 initial
 (op (car sequence)
 (accumulate op initial (cdr sequence)))))

 (define (map p sequence)
 (accumulate (lambda (x y) (cons (p x) y)) null sequence))
 (define (append seq1 seq2)
 (accumulate cons seq1 seq2))
 (define (length sequence)
 (accumulate (lambda (x y) (add1 y)) 0 sequence))

Ok, there’s a little difference.

My result:

> (append '(1 2 3) '(4 5 6))
'(4 5 6 1 2 3)

(define (append seq1 seq2)
    (accumulate cons seq2 seq1))

> (append '(1 2 3) '(4 5 6))
'(1 2 3 4 5 6)

2.34

The initial number is zero, which multiplied by x equals zero. Thus it can be used as the initial number.

(list 1 3 0 5 0 1) -> 1 + 3x + 5x^3 + x^5.

This is (+ (* (3 + 5x^2 + x^4) x) 1)) -> (+ (* higher-terms x) this-coeff)), as thisCoeff is the initial number.

……

 (define (horner-eval x coefficient-sequence)
 (accumulate (lambda (this-coeff higher-terms) (+ (* higher-terms x) this-coeff))
 0
 coefficient-sequence))

2.35

map? Ok, use itself.

 (define (count-leaves t)
 (accumulate + 0 (map 
 (lambda (tree)
 	(if (pair? tree)
 		(count-leaves tree)
 		1
 	)
 ) t)))

2.36

Abstraction!

(define (accumulate-n op init seqs)
 (if (null? (car seqs))
 null
 (cons (accumulate op init 
    (accumulate (lambda (x y) (cons (car x) y)) null seqs)
 )
 (accumulate-n op init 
    (accumulate (lambda (x y) (cons (cdr x) y)) null seqs)
 ))))

> (accumulate (lambda (x y) (cons (car x) y)) null '((1 2 3) (4 5 6) (7 8 9) (10 11 12)))
'(1 4 7 10)
> (accumulate (lambda (x y) (cons (cdr x) y)) null '((1 2 3) (4 5 6) (7 8 9) (10 11 12)))
'((2 3) (5 6) (8 9) (11 12))

> (accumulate-n + 0 '((1 2 3) (4 5 6) (7 8 9) (10 11 12)))
'(22 26 30)

There’s an alternative solution, nevermind.

(define (car-n seqs)
    (map car seqs))
(define (cdr-n seqs)
    (map cdr seqs))

(define (accumulate-n op init seqs)
    (if (null? (car seqs))
        '()
        (cons (accumulate op init (car-n seqs))
              (accumulate-n op init (cdr-n seqs)))))

2.37

So the accumulate is designed for matrices, and they fit each other perfectly.

(define (dot-product v w)
 (accumulate + 0 (map * v w)))

(define (matrix-*-vector m v)
 (map (lambda (w) (dot-product v w)) m))

(define (transpose mat)
 (accumulate-n cons null mat))

(define (matrix-*-matrix m n)
 (let ((cols (transpose n)))
 (map (lambda (v) (matrix-*-vector cols v)) m)))

2.38

(define (fold-right op initial sequence)
 (if (null? sequence)
 initial
 (op (car sequence)
 (fold-right op initial (cdr sequence)))))

(define (fold-left op initial sequence)
 (define (iter result rest)
 (if (null? rest)
 result
 (iter (op result (car rest))
 (cdr rest))))
 (iter initial sequence))

Obviously, fold-left is tail-recursive. We’d use it more.

Which remind me of OCaml, although this must be earlier.

>  (fold-left list null (list 1 2 3))
'(((() 1) 2) 3)
>  (fold-right list null (list 1 2 3))
'(1 (2 (3 ())))

The last two examples demonstrated clearly: Only when the exchange rule is permitted in the operation could these two functions work the same.

Oh, associative law or monoid( maybe more exactly: semigroup).

2.39

(define (reverse sequence)
 (fold-right (lambda (x y) (append y (list x))) nil sequence))

(define (reverse sequence)
 (fold-left (lambda (x y) (cons y x)) nil sequence))

2.40

(define (flatmap proc seq)
  (accumulate append nil (map proc seq)))

(define (unique-pairs n)
	(flatmap (lambda (i)
          (map (lambda (j) 
                 (list i j))
               (enumerate-interval 1 (- i 1))))
        (enumerate-interval 1 n))
)

2.41

distinct positive integers.

(define (three-sum n s)
	(map
		(lambda (pair)
			(cons (- s (+ (car pair) (cadr pair))) pair)
		)
		(filter 
			(lambda (pair) (< (+ (car pair) (cadr pair)) s ))
        	(unique-pairs n)
		)
	)
)

This one above produces some duplicate answers.

Just another brainless one.

(define (unique-three n)
	(flatmap (lambda (i)
          (flatmap (lambda (j) 
                 (map (lambda (k)
                 	(list i j k)
                 )
                 (enumerate-interval 1 (- j 1))
                 )
                 )
               (enumerate-interval 1 (- i 1))))
        (enumerate-interval 1 n))
)

(define (three-sum n s)
	(filter
		(lambda (l) (= (+ (car l)  (car (cdr l))  (car (cdr (cdr l))))  s))
        (unique-three n)
	)
)

OK, then. We need more abstactions.

(define (triple-sum-equal-to? sum triple)
    (= sum
       (+ (car triple)
          (cadr triple)
          (caddr triple))))

(define (triple-sum-equal-to? sum triple)
    (= sum
       (fold-right + 0 triple)))

2.42

Here comes the old friend.

adjoin-position simply add all the possible places for the queen to the rest of queens places.

(define (adjoin-position r c rest-of-queens)
	(cons (list r c) rest-of-queens)
)

(define empty-board null)

(= a-c b-c) will never break. Never mind.

(define (cross a b)
	(let ((a-r (car a)) (a-c (cadr a)) (b-r (car b)) (b-c (cadr b)))
		(if (or (= a-r b-r) (= a-c b-c))
			#t
			(if (= (abs (- a-r b-r)) (abs (- a-c b-c)))
				#t
				#f
			)
	    )
    )
)

(define (safe? k positions)
	(if (< (length positions) 2)
		#t
		(let ((new-queen (car positions)))
		(define (aux rest)
			(if (null? rest)
				#t
				(if (cross new-queen (car rest))
					#f
					(aux (cdr rest))
			)
			)

		)
		(aux (cdr positions))
		)
	)
)

The K in parameter is useless. Why?

(define (queens board-size)
  (define (queen-cols k)
    (if (= k 0)
        (list empty-board)
        (filter
         (lambda (positions) 
           (safe? k positions))
         (flatmap
          (lambda (rest-of-queens)
            (map (lambda (new-row)
                   (adjoin-position 
                    new-row 
                    k 
                    rest-of-queens))
                 (enumerate-interval 
                  1 
                  board-size)))
          (queen-cols (- k 1))))))
  (queen-cols board-size))

OK.

(define (adjoin-position new-row k rest-of-queens)
    (cons new-row rest-of-queens))

(define (safe? k position)
    (iter-check (car position) 
                (cdr position)
                 1))

(define (iter-check row-of-new-queen rest-of-queens i)
    (if (null? rest-of-queens)  ; 下方所有皇后检查完毕，新皇后安全
        #t
        (let ((row-of-current-queen (car rest-of-queens)))
            (if (or (= row-of-new-queen row-of-current-queen)           ; 行碰撞
                    (= row-of-new-queen (+ i row-of-current-queen))     ; 右下方碰撞
                    (= row-of-new-queen (- row-of-current-queen i)))    ; 左下方碰撞
                #f
                (iter-check row-of-new-queen 
                            (cdr rest-of-queens)    ; 继续检查剩余的皇后
                            (+ i 1))))))            ; 更新步进值

2.43

Louis Reasoner is having a terrible time doing Exercise 2.42.

Well, actually terrible.

Louis exchanged the order of generating all possibilities and checking safety, such as generating all the placement possibilities for all the queens and then checking them, while our procedure will check the safety when placing each new queen.

练习 2.42 的 queens 函数对于每个棋盘 (queen-cols k) ，使用 enumerate-interval 产生 board-size 个棋盘。
而 Louis 的 queens 函数对于 (enumerate-interval 1 board-size) 的每个 k ，都要产生 (queen-cols (- k 1)) 个棋盘。
因此， Louis 的 queens 函数的运行速度大约是原来 queens 函数的 board-size 倍，也即是 T * board-size 。

Really? Their speed of producing the (n-1) board-size is different.

thongpv87
@aQuaYi I don’t think it is correct because number of queen-cols also change over time

https://wernerdegroot.wordpress.com/2015/08/01/sicp-exercise-2-43/

LOL. I need a standard solution.

2.44

(define (right-split painter n)
  (if (= n 0)
      painter
      (let ((smaller (right-split painter 
                                  (- n 1))))
        (beside painter 
                (below smaller smaller)))))

(define (up-split painter n)
  (if (= n 0)
      painter
      (let ((smaller (right-split painter 
                                  (- n 1))))
        (below painter 
                (beside smaller smaller)))))

2.45

(define (split one two)
	(define (aux painter n)
		  (if (= n 0)
      		painter
      		(let ((smaller (aux painter 
                                  (- n 1))))
        		(one painter 
                		(two smaller smaller)))))
	)
	(lambda (painter n)
		(aux painter n)
	)
)

Oh, there’s no need for another lambda.

(define (split big-combiner small-combiner)
    (define (inner painter n)
        (if (= n 0)
            painter
            (let ((smaller (inner painter (- n 1))))
                (big-combiner painter   
                              (small-combiner smaller smaller)))))
    inner)

2.46

(define make-vect cons)

(define xcor-vect car)

(define (ycor-vect v)
	(cdr v)
)

(define (add-vect v1 v2)
	(make-vect
		(+ (xcor-vect v1) (xcor-vect v2))
		(+ (ycor-vect v1) (ycor-vect v2))
	)
)

(define (sub-vect v1 v2)
	(make-vect
		(- (xcor-vect v1) (xcor-vect v2))
		(- (ycor-vect v1) (ycor-vect v2))
	)
)

(define (scale-vect n v)
	(make-vect
		(* (xcor-vect v) n)
		(* (ycor-vect v) n)
	)
)

2.47

(define (make-frame origin edge1 edge2)
 (list origin edge1 edge2))
(define (origin frame)
	(car frame)
)
(define (edge1 frame)
	(car (cdr frame))
)

(define (edge2 frame)
	(car (cdr (cdr frame)))
)

(define (make-frame origin edge1 edge2)
 (cons origin (cons edge1 edge2)))
 
(define (origin frame)
	(car frame)
)
(define (edge1 frame)
	(car (cdr frame))
)

(define (edge2 frame)
	(cdr (cdr frame))
)

2.48

(define (make-segment v1 v2)
	(cons v1 v2)
)
(define start-segment
	car
)
(define end-segment
	cdr
)

2.49

How to select edges of a frame?

All the solutions I find are not proper. The book means vector graph, you know?

(define (segments->painter segment-list)
 (lambda (frame)
 (for-each
 (lambda (segment)
 (draw-line
 ((frame-coord-map frame)
 (start-segment segment))
 ((frame-coord-map frame)
 (end-segment segment))))
 segment-list)))

(define (outline frame)
	(let ((outlines (list 
		(make-segment (origin frame) (add-vect (origin frame) (edge1 frame)) ) 
		(make-segment (origin frame) (add-vect (origin frame) (edge2 frame)) ) 
		(make-segment (add-vect (origin frame) (edge2 frame)) (add-vect (add-vect (origin frame) (edge2 frame)) (edge1 frame)) ) 
		(make-segment (add-vect (origin frame) (edge1 frame)) (add-vect (add-vect (origin frame) (edge1 frame)) (edge2 frame)) )
		)))
		(segments->painter outlines)
	)
)

So, this is a problem about frame vectors transformation.

(define (top-left frame)
	(add-vect (origin frame) (edge2 frame))
)

(define (top-right frame)
	(add-vect (add-vect (origin frame) (edge2 frame)) (edge1 frame))
)

(define (bot-right frame)
	(add-vect (origin frame) (edge1 frame))
)

(define bot-left origin)

(define (draw-x frame)
	(let ((outlines (list 
		(make-segment (top-left frame) (bot-right frame))
		(make-segment (bot-left frame) (top-right frame))
		)))
		(segments->painter outlines)
	)
)

(define (left-mid frame)
	(add-vect (origin frame) (scale-vect 0.5 (edge2 frame))
)

(define (top-mid frame)
	(add-vect (add-vect (origin frame) (edge2 frame)) (scale-vect 0.5 (edge1 frame))
)

(define (right-mid frame)
	(add-vect (add-vect (origin frame) (edge1 frame)) (scale-vect 0.5 (edge2 frame))
)

(define (bot-mid frame)
	(add-vect (origin frame) (scale-vect 0.5 (edge1 frame))
)

(define (draw-x frame)
	(let ((outlines (list 
		(make-segment (left-mid frame) (top-mid frame))
		(make-segment (top-mid frame) (right-mid frame))
		(make-segment (right-mid frame) (bot-mid frame))
		(make-segment (bot-mid frame) (left-mid frame))
		)))
		(segments->painter outlines)
	)
)

What the…

I didn’t find the definition of wave.

2.50

(define (flip-horiz painter)
 (transform-painter painter
 (make-vect 1.0 0.0) 
 (make-vect 0.0 0.0) 
 (make-vect 1.0 1.0))) 

(define (rotate90 painter)
 (transform-painter painter
 (make-vect 1.0 1.0)
 (make-vect 0.0 1.0)
 (make-vect 1.0 0.0)))

(define (rotate270 painter)
 (transform-painter painter
 (make-vect 0.0 1.0)
 (make-vect 0.0 0.0)
 (make-vect 1.0 1.0)))

2.51

(define (below painter1 painter2)
 (let ((split-point (make-vect 0.0 0.5)))
 (let ((paint-bot
 painter1
 (transform-painter
 (make-vect 0.0 0.0)
 (make-vect 1.0 0.0)
 split-point
 ))
 (paint-top
 (transform-painter
 painter2
 split-point
 (make-vect 1.0 0.5)
 (make-vect 0.0 1.0))))
 (lambda (frame)
 (paint-bot frame)
 (paint-top frame)))))

(define (below painter1 painter2)
	(lambda (frame)
		(rotate270 (beside (rotate90 paint1) (rotate90 paint2))	)
	)
)

2.52

 (define (corner-split painter n)
 (if (= n 0)
 painter
 (let ((up (up-split painter (- n 1)))
 (right (right-split painter (- n 1))))
 (let ((top-left up)
 (bottom-right right)
 (corner (corner-split painter (- n 1))))
 (beside (below painter top-left)
 (below bottom-right corner))))))

You need some rotations.

2.53

Welcome to Racket v7.9 [bc].
> (list 'a 'b 'c)
'(a b c)
>  (list (list 'george))
'((george))
>  (cdr '((x1 x2) (y1 y2)))
'((y1 y2))
>  (cadr '((x1 x2) (y1 y2)))
'(y1 y2)
>  (pair? (car '(a short list)))
#f
>  (memq 'red '((red shoes) (blue socks)))
#f
>  (memq 'red '(red shoes blue socks))
'(red shoes blue socks)

>  (cadr '((x1 x2) (y1 y2)))
'(y1 y2)

The bracket in quotaiton still makes sense.

2.3

2.54

(define (equal? a b)
    (cond
        ((number? a) (and (number? b) (eq? a b)))
        ((number? b) (and (number? a) (eq? a b)))
        ((null? a) (null? b))
        ((null? b) (null? a))
        ((and (number? (car a)) (number? (car b))) (and (eq? (car a) (car b)) (equal? (cdr a) (cdr b))))
        ((and (list? (car a)) (list? (car b))) (and (equal? (car a) (car b)) (equal? (cdr a) (cdr b))))
        (else false)
    )
)

2.55

Confusing…

'abracadabra -> (quote abracadabra) -> abracadabra itself, which is not a list.

> (car 'abracadabra)
; car: contract violation
;   expected: pair?
;   given: 'abracadabra
; [,bt for context]

''abracadabra -> (quote (quote abracadabra))

So we also would see that element in the list is not evaluated at once.

> (cdr ''abracadabra)
'(abracadabra)
> (car ''abracadabra)
'quote

2.56

I’m about to ask this question.

(define (deriv exp var)
 (cond ((number? exp) 0)
 ((variable? exp) (if (same-variable? exp var) 1 0))
 ((sum? exp) (make-sum (deriv (addend exp) var)
 (deriv (augend exp) var)))
 ((product? exp)
 (make-sum
 (make-product (multiplier exp)
 (deriv (multiplicand exp) var))
 (make-product (deriv (multiplier exp) var)
 (multiplicand exp))))
 ((exponentiation? exp)
    (make-product 
        (make-product (exponent exp) (make-exponentiation (base exp) (make-sum (exponent exp) -1))) 
        (deriv (base exp) var)
    )
 )
 (else
 (error "unknown expression type: DERIV" exp))))


(define (exponentiation? s)
    (and (pair? s) (eq? (car s) '**))
)

(define (base s)
    (cadr s)
)

(define (exponent s)
    (caddr s)
)

(define (make-exponentiation m1 m2)
 (cond
 ((=number? m1 0) 0)
 ((=number? m1 1) 1)
 ((=number? m2 1) m1)
 ((=number? m2 0) 1)
 ((and (number? m1) (number? m2)) (expt m1 m2))
 (else (list '** m1 m2))))

> (deriv (make-exponentiation 'x 1) 'x)
1
> (deriv (make-exponentiation 'x 2) 'x)
'(* 2 x)
> (deriv (make-exponentiation 'x 3) 'x)
'(* 3 (** x 2))
> (deriv (make-exponentiation 'x 4) 'x)
'(* 4 (** x 3))

However.

> (deriv (make-exponentiation 2 'x) 'x)
0

2.57

How to represent scalable param?

Oh, we don’t need rewrite make-sum and make-product, our params are always legal.

(define (augend s)
    (if (> (length s) 3)
        (cons '+ (cddr s))
        (caddr s)
    )
)

(define (multiplicand p)
    (if (> (length s) 3)
        (cons '* (cddr s))
        (caddr s)
    )
)

> (deriv '(* x y (+ x 3)) 'x)
'(+ (* x y) (* y (+ x 3)))

2.58

Because of the abstraction barrier, there is no need to modify deriv.

(define (make-sum a1 a2)
 (cond ((=number? a1 0) a2)
 ((=number? a2 0) a1)
 ((and (number? a1) (number? a2))
 (+ a1 a2))
 (else (list a1 '+ a2))))
 
(define (sum? x) (and (pair? x) (eq? (cadr x) '+)))

(define (addend s) (car s))
(define (augend s) (caddr s))

(define (make-product m1 m2)
 (cond ((or (=number? m1 0) (=number? m2 0)) 0)
 ((=number? m1 1) m2)
 ((=number? m2 1) m1)
 ((and (number? m1) (number? m2)) (* m1 m2))
 (else (list m1 '* m2))))
 
(define (product? x) (and (pair? x) (eq? (cadr x) '*)))

(define (multiplier p) (car p))
(define (multiplicand p) (caddr p))

> (deriv '(x + (3 * (x + ( y + 2 )))) 'x)
4

We need more bracket. We need context to know if we could execute the numbers so far.

2.59

We are waiting for the heap, right?

(define (union-set a b)
    (if (null? a)
        b
        (union-set (cdr a) (adjoin-set (car a) b))
    )
)

2.60

(define (element-of-set? x set)
 (cond ((null? set) false)
 ((equal? x (car set)) true)
 (else (element-of-set? x (cdr set)))))

(define (adjoin-set x set)
	(cons x set)
)

(define (intersection-set set1 set2)
 (cond ((or (null? set1) (null? set2)) '())
 ((element-of-set? (car set1) set2)
 (cons (car set1) (intersection-set (cdr set1) set2)))
 (else (intersection-set (cdr set1) set2))))

(define (union-set a b)
    (if (null? a)
        b
        (union-set (cdr a) (adjoin-set (car a) b))
    )
)

2.61

(define (adjoin-set x set)
	(cond
    	((null? set) (list x))
        ( (= (car set) x) set )
		( (> (car set) x) (cons x set) )
		(else (cons x (adjoin-set x (cdr set)) ))
	)
)

LOL.

(define (adjoin-set x set)
    (union-set (list x) set))

2.62

The pattern is like intersection-set.

(define (union-set set1 set2)
  (if (or (null? set1) (null? set2))
      '()
      (let ((x1 (car set1)) (x2 (car set2)))
        (cond ((= x1 x2)
               (cons x1 (union-set 
                         (cdr set1)
                         (cdr set2))))
              ((< x1 x2) 
               (cons x1 (union-set 
                          (cdr set1) 
                          set2)))
              ((< x2 x1) 
              	(consx x2 (union-set 
                          set1 
                          (cdr set2))))
        )
      )
  )
)

2.63

It seems both two have the same order: left -> mid -> right.

(1 2 3 4 5 6 7)
Obviously, the second one is better. It doesn’t use append.

tree->list-1 的复杂度为 Θ(n^2) 。
tree->list-2 的复杂度为 Θ(n) 。

2.64

It utilizes the power of recursion. The function partitions the entire list into three parts: left-tree, this entry, and right-tree, and recursively calls the function with the designated number of elements to construct the sub-trees until there’s only one element left of no element left. Then the tree is itself. Surprisingly, it doesn’t consume extra memory. Once the function constructs a new tree, it conses the tree to the head of the given elements’ list and return it. So the caller can use it directly. The result:
```
> (quotient (- 6 1) 2)
2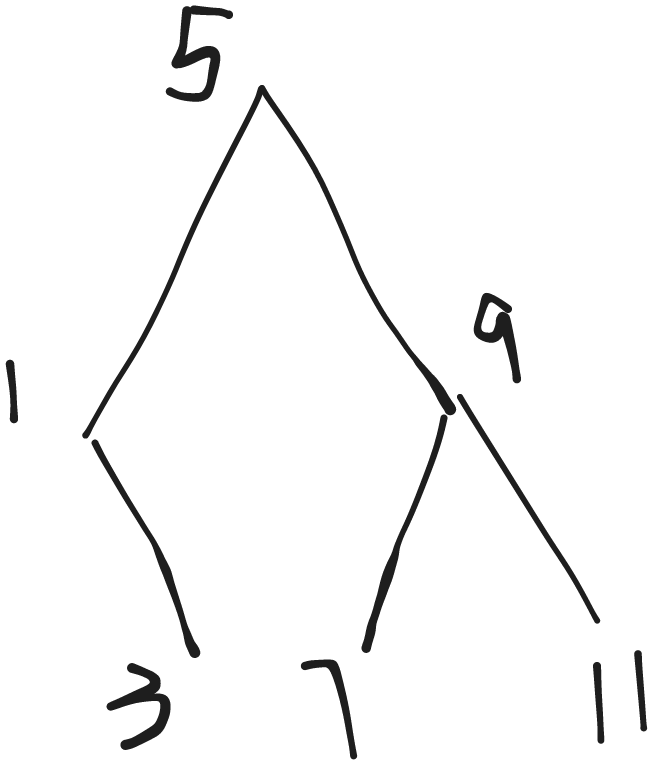
   
```
O(n)

2.65

I copied the answers which are dumb. The problem is too tedious, surly it has more efficient answers.

(define (intersection-tree tree another)
    (list->tree
        (intersection-set (tree->list-2 tree)
                          (tree->list-2 another))))

(define (union-tree tree another)
    (list->tree
        (union-set (tree->list-2 tree)
                   (tree->list-2 another))))

2.66

Just like element-of-set?, right?

(define (element-of-set? x set)
 (cond ((null? set) false)
 ((= x (entry set)) true)
 ((< x (entry set))
 (element-of-set? x (left-branch set)))
 ((> x (entry set))
 (element-of-set? x (right-branch set)))))

(define (lookup given-key set)
 (cond ((null? set) false)
 ((equal? given-key (key (entry set))) (entry set))
 ((< given-key (key (entry set)))
 (lookup given-key (left-branch set)))
 ((> given-key (key (entry set)))
 (lookup given-key (right-branch set)))))

2.67

> (decode sample-message sample-tree)
'(A D A B B C A)

2.68

(define (decode bits tree)
  (define (decode-1 bits current-branch)
    (if (null? bits)
        '()
        (let ((next-branch
               (choose-branch 
                (car bits) 
                current-branch)))
          (if (leaf? next-branch)
              (cons 
               (symbol-leaf next-branch)
               (decode-1 (cdr bits) tree))
              (decode-1 (cdr bits) 
                        next-branch)))))
  (decode-1 bits tree))
  
(define (choose-branch bit branch)
  (cond ((= bit 0) (left-branch branch))
        ((= bit 1) (right-branch branch))
        (else (error "bad bit: 
               CHOOSE-BRANCH" bit))))

According to the decode, especially choose-branch, which implies that left is zero and right is 1.

(define (element-of-set? x set)
  (cond ((null? set) false)
        ((equal? x (car set)) true)
        (else (element-of-set? x (cdr set)))))

(define (encode-symbol s tree)
    (define (aux code branch remain)
        (cond
            ((null? remain) code)
            ((leaf? branch)	
                (aux code tree (cdr remain))
            )
            ((element-of-set? (car remain) (symbols (left-branch branch)))
                (aux (cons '0 code) (left-branch branch) remain)
            )
            ((element-of-set? (car remain) (symbols (right-branch branch)))
                (aux (cons '1 code) (right-branch branch) remain)
            )
            (else (error "no branch!"))
        )
    )
    (aux null tree s)
)

> (encode-symbol (decode sample-message sample-tree) sample-tree)
'(0 1 1 1 0 1 0 1 0 0 1 1 0)
> sample-message
'(0 1 1 0 0 1 0 1 0 1 1 1 0)

2.69

You can take significant advantage of the fact that we are using an ordered set representation.)

The first two tree is the smallest two.

(define (successive-merge ordered-set)
    (cond ((= 0 (length ordered-set))
            '())
          ((= 1 (length ordered-set))
            (car ordered-set))
          (else
            (let ((new-sub-tree (make-code-tree (car ordered-set)
                                                (cadr ordered-set)))
                  (remained-ordered-set (cddr ordered-set)))
                (successive-merge (adjoin-set new-sub-tree remained-ordered-set))))))

2.70

Come on, caps! bro…

> (encode-symbol '(GET A JOB SHA NA NA NA NA NA NA NA NA GET A JOB SHA NA NA NA NA NA NA NA NA WAH YIP YIP YIP YIP YIP YIP YIP YIP YIP SHA BOOM) tree)

'(1 1 0 1 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 1)

8 = 2^3. So we need 3 bits for every word, then 36*3 = 108. More than 84 of Huffman tree.

2.71

1 + 2 + 4 +...+ 2^(n-1) < 2^n, So the most frequent symbol only needs 1 bit to represent. And thus the lest frequent symbol needs (n-1) bits.

2.72

The general Huffman tree is supposed to be balanced, while the 2.71 example is most unbalanced.

As the 2.71 described, the most frequent: 1 * n -> O(n), the lest frequent: (n-1) * n -> O(n^2). But the least frequent won’t appear that much cause it’s the least frequent. Maybe that’s why the general order of growth of Huffman is complicated.

2.4

2.73

Because there’s no tag, or operator.

Could you just send the exp in? I must reimplement multiplier, multiplicand series again.

(define (install-deriv-package)
 ;; internal procedures
(define (make-sum a1 a2)
 (cond ((=number? a1 0) a2)
 ((=number? a2 0) a1)
 ((and (number? a1) (number? a2))
 (+ a1 a2))
 (else (list '+ a1 a2))))
(define (=number? exp num) (and (number? exp) (= exp num)))

(define (make-product m1 m2)
 (cond ((or (=number? m1 0) (=number? m2 0)) 0)
 ((=number? m1 1) m2)
 ((=number? m2 1) m1)
 ((and (number? m1) (number? m2)) (* m1 m2))
 (else (list '* m1 m2))))

(define (sum? x) (and (pair? x) (eq? (car x) '+)))

(define (addend s) (cadr s))

 (define (augend s) (caddr s))

 (define (product? x) (and (pair? x) (eq? (car x) '*)))

 (define (multiplier p) (cadr p))

 (define (multiplicand p) (caddr p))

 (define (plus-deriv exp var)
 (make-sum
 (make-product (car exp)
 (deriv (cadr exp) var))
 (make-product (deriv (car exp) var)
 (cadr exp)))
 ) 
 (define (product-deriv exp var)
 (make-sum
 (make-product (car exp)
 (deriv (cadr exp) var))
 (make-product (deriv (car exp) var)
 (cadr exp)))
 )
 ;; interface to the rest of the system
 (put 'deriv '(+) plus-deriv)
 (put 'deriv '(*) product-deriv)
 'done)

 (define (make-exponentiation m1 m2)
 (cond
 ((=number? m1 0) 0)
 ((=number? m1 1) 1)
 ((=number? m2 1) m1)
 ((=number? m2 0) 1)
 ((and (number? m1) (number? m2)) (expt m1 m2))
 (else (list '** m1 m2))))
 (define (exponent-deriv exp var)
    (make-product 
        (make-product (cadr exp) (make-exponentiation (car exp) (make-sum (cadr exp) -1))) 
        (deriv (car exp) var)
    )
 )
 
 (put 'deriv '(**) product-deriv)

(get ⟨op⟩ ⟨type⟩)

(get 'deriv (operator exp)) (operands exp) var) -> ` ((get (operator exp) ‘deriv) (operands exp) var)`

It’s not the plus in deriv package, but the deriv in operator package.

(put ⟨op⟩ ⟨type⟩ ⟨item⟩)

(put '(+) 'deriv plus-deriv)
(put '(*) 'deriv product-deriv)

2.74

Is the context needed?

OK, it’s still not enough. Shall I define the record?

Every division needs to implement its own get-record method and put.

(define (get-record name division)
 ((get 'get-record division) name))

(define (get-salary name record)
 ((get 'get-salary division) record))

Just implement a new set of methods for the new company.

2.75

(define (make-from-mag-ang r a)
 (define (dispatch op)
 (cond ((eq? op 'real-part)  (* (magnitude z) (cos (angle z))))
 ((eq? op 'imag-part)  (* (magnitude z) (sin (angle z))))
 ((eq? op 'magnitude) r)
 ((eq? op 'angle) a)
 (else (error "Unknown op: MAKE-FROM-REAL-IMAG" op))))
 dispatch)

2.76

The question ask us which method is type-oriented and which one is operation-oriented.

In my opinion, message passing is better in adding new type, but it’s annoying to add new method cause you need to add the new operation to every type.

Data-directed is good at adding new method. OK, maybe both adding is convenient.

数据导向：数据导向可以很方便地通过包机制增加新类型和新的通用操作，因此无论是增加新类型还是增加新操作，这种策略都很适合。

2.5

2.77

The magnitude isn’t added in the interface, thus it won’t work.

how many times is apply-generic invoked?

Twice.

What procedure is dispatched to in each case?

First to magnitude in Complex, then to magnitude-rectangular in Rectangular.

2.78

Like this? It’s not convenient, the main package body still needs to use the generic procedure. Although it reduce the memory usage.

(define (attach-tag type-tag contents)
 (cond
  ((number? contents) contents)
  (else (cons type-tag contents))
 )
)
(define (type-tag datum)
 (cond
    ((pair? datum) (car datum))
    ((number? datum) 'scheme-number)
    (else (error "Bad tagged datum: TYPE-TAG" datum))
 ))

(define (contents datum)
    (cond 
 ((pair? datum) (cdr datum))
 ((number? datum) datum)
 (error "Bad tagged datum: CONTENTS" datum)))

2.79

Could we distinguish a generic from normal pairs?

This operation should work for ordinary numbers, rational numbers, and complex numbers.

OK, fair enough.

(define (equ? a b)
	(cond 
        ((and (number? a) (number? b)) (equal? a b))
        ((and (pair? a) (pair? b)) 
            (and (equal? (type-tag a) (type-tag b)) (equal? (contents a) (contents b)))
        )
    )
)

(define (equ? x y)
    (apply-generic 'equ? x y))

I get it, every type should implement its own equal, cause maybe two different contents could be equal. Like 1/2 and 2/4.

2.80

So, this one should also be the generic function.

(define (=zero? x)
    (apply-generic '=zero? x))

    (put '=zero? '(scheme-number)
        (lambda (value)
            (= value 0)))

    (put '=zero? '(rational)
        (lambda (r)
            (= 0 (numer r))))

(put '=zero? '(complex)
    (lambda (c)
        (and (= 0 (real-part c))
             (= 0 (imag-part c)))))

2.81

complex seems just throw a error, while scheme-number would loop infinitely.

She’s wrong. The apply-generic doesn’t need this. Moreover, this could cause infinite loop cause scheme-number would try to convert itself to itself infinitely.

I’m not sure if this is necessary, two same types would end in the else branch of inner cond.

(define (apply-generic op . args)
  (let ((type-tags (map type-tag args)))
    (let ((proc (get op type-tags)))
      (if proc
          (apply proc (map contents args))
          (if (= (length args) 2)
              (let ((type1 (car type-tags))
                    (type2 (cadr type-tags))
                    (a1 (car args))
                    (a2 (cadr args)))
                (let ((t1->t2 (get-coercion type1 type2))
                      (t2->t1 (get-coercion type2 type1)))
                  (cond 
                  		((equal? type1 type2) (error "No method for these types"
                                (list op type-tags)))
                  		(t1->t2
                         (apply-generic op (t1->t2 a1) a2))
                        (t2->t1
                         (apply-generic op a1 (t2->t1 a2)))
                        (else
                         (error "No method for these types"
                                (list op type-tags))))))
              (error "No method for these types"
                     (list op type-tags)))))))

2.82

I’m not sure if there exists a method which needs two different types. Like a method named eat which needs a dog and a piece of food. In this case the conversion is not capable.

Show how to generalize apply-generic to handle coercion in the general case of multiple arguments.

Maybe not. I need another method to recursively modify the list and test whether it can be processed.

2.83

(put 'raise '(scheme-number)
 (lambda (x) 
   (make-rat x 1)
 )
)

real? Do we have real yet?

(put 'raise '(rational)
 (lambda (x) 
    (* 1.0 (/ (numer x) (denom x)))
 )
)

(put 'raise '(real)
 (lambda (x) 
   (make-complex-from-real-imag x 0)
 )
)

2.84

My implement in last problem is not capable in this one, I need to rewrite it. Also, we need to maintain a tower hierarchy of the types, which should be a list. Troublesome.

(define number-tower '(scheme-number realrational real complex))

(define (raise-left type1 type2)
    (let ((type1-hi (memq type1 number-tower)) (type2-hi (memq type2 number-tower)))
        (if (and type1-hi type2-hi (< (length type1-hi) (length type2-hi))))
    )
)

(define (raise-right type1 type2)
    (let ((type1-hi (memq type1 number-tower)) (type2-hi (memq type2 number-tower)))
        (if (and type1-hi type2-hi (> (length type1-hi) (length type2-hi))))
    )
)

(define (apply-generic op . args)
  (let ((type-tags (map type-tag args)))
    (let ((proc (get op type-tags)))
      (if proc
          (apply proc (map contents args))
          (if (= (length args) 2)
              (let ((type1 (car type-tags))
                    (type2 (cadr type-tags))
                    (a1 (car args))
                    (a2 (cadr args)))
                (let ((raise-t1 
                       (raise-left type1 type2))
                      (raise-t2 
                       (raise-right type1 type2)))
                  (cond (raise-t1
                         (apply-generic 
                          op (raise a1) a2))
                        (raise-t2
                         (apply-generic 
                          op a1 (raise a2)))
                        (else
                         (error 
                          "No method for 
                           these types"
                          (list 
                           op 
                           type-tags))))))
              (error 
               "No method for these types"
               (list op type-tags)))))))

2.85

2.86

2.87

(define (=zero? x)
    (apply-generic '=zero? x))

    (put '=zero? '(scheme-number)
        (lambda (value)
            (= value 0)))

    (put '=zero? '(rational)
        (lambda (r)
            (= 0 (numer r))))

(put '=zero? '(complex)
    (lambda (c)
        (and (= 0 (real-part c))
             (= 0 (imag-part c)))))

(put '=zero? '(polynomial)
    (lambda (c)
    	(if (empty-termlist? c)
    		#t
    		(and (=zero (coeff (first-term c))) (=zero? (rest-terms c)))
    	)
    )
)

2.88

(define (negation p)
	(define (negation-terms terms)
		(let ((first (first-term terms)))
		(adjoin-term (make-term (order first) (- (coeff first)))
			(negation-terms (rest-terms terms))
		)
		)
	)
	(if (empty-termlist? (term-list p))
		p
		(make-poly (variable p) (negation-terms (term-list p)))
	)
)

(define (sub-poly p1 p2)
	(add-poly p1 (negation p2))
)

2.89

The term related procedures couldn’t rewrite, thus there are much unnecessary cost, or I should rewrite the whole package. Maybe there are some better cut-in point.

(define (adjoin-term term term-list)
  (if (=zero? (coeff term))
      term-list
      (
      	if (= (length term-list) (order term))
      		(cons (coeff term) term-list)
      		(adjoin-term term (cons 0 term-list))
      )))

(define (the-empty-termlist) '())

(define (first-term term-list) (make-term (- (length term-list) 1) (car term-list)))

(define (rest-terms term-list) (cdr term-list))

(define (empty-termlist? term-list) 
  (null? term-list))

(define (make-term order coeff) 
  (list order coeff))

(define (order term) (car term))
(define (coeff term) (cadr term))

2.90

Tag tag tag.

Only adjoin-term and first-term need to be generic, which is a little wired. Or should I package all the procedures twice? This would be duplicate.

(define (adjoin-term term term-list)
  (if (=zero? (coeff term))
      term-list
      (
      	if (= (length term-list) (order term))
      		(cons (coeff term) term-list)
      		(adjoin-term term (cons 0 term-list))
      )))
(define (first-term term-list) (make-term (- (length term-list) 1) (car term-list)))

(define (tag p) (attach-tag 'dense p))
(put 'make-poly 'dense
	(lambda (var terms) (tag (make-poly var terms))))
(put 'adjoin-term '(dense) adjoin-term)
(put 'first-term '(dense) first-term)

(define (adjoin-term term term-list)
  (if (=zero? (coeff term))
      term-list
      (cons term term-list)))
(define (first-term term-list) (car term-list))

(define (tag p) (attach-tag 'sparse p))

(define (tag p) (attach-tag 'sparse p))
(put 'make-poly 'sparse
	(lambda (var terms) (tag (make-poly var terms))))
(put 'adjoin-term '(sparse) adjoin-term)
(put 'first-term '(sparse) first-term)

2.91

	(define (negation-terms terms)
		(let ((first (first-term terms)))
		(adjoin-term (make-term (order first) (- (coeff first)))
			(negation-terms (rest-terms terms))
		)
		)
	)

This procedure returns (list quotient remainder)

(define (div-terms L1 L2)
  (if (empty-termlist? L1)
      (list (the-empty-termlist) 
            (the-empty-termlist))
      (let ((t1 (first-term L1))
            (t2 (first-term L2)))
        (if (> (order t2) (order t1))
            (list (the-empty-termlist) L1)
            (let ((new-c (div (coeff t1) 
                              (coeff t2)))
                  (new-o (- (order t1) 
                            (order t2))))
              (let ((rest-of-result
                     (div-terms 
                     	(add-terms L1 
                     		(negation-terms 
                     			(mul-terms 
                     				(list (make-term new-o new-c))
                     				L2
                     				))) L2)
                     ))
               (list (adjoin-term (make-term new-o new-c) (car rest-of-result)) 
                	(cadr rest-of-result))
                    ))))))

2.92

imposing an ordering on variables

What order? I don’t get it.

I kind of get it, any certain order could make sense, we need to reform a canonical form when there are different variables. I hide lower ordered variable in the coefficient of the higher_var^0.

How to extract a potential variable from the coefficients? Or should I make the make-poly returns a ordered poly?

We must ensure every poly is constructed with variables in order.

Maybe not. This answer not finished. I tried.

I need 'add '(polynomial scheme-number), 'multiply '(polynomial scheme-number).

(define (tag p) (attach-tag 'polynomial p))
(put 'add '(polynomial polynomial)
	(lambda (p1 p2) (tag (add-poly p1 p2))))
(put 'mul '(polynomial polynomial)
	(lambda (p1 p2) (tag (mul-poly p1 p2))))

(define (variable<? v1 v2)
  (string<? (symbol->string v1) (symbol->string v2)))

(define (canonical v p)
    (make-poly v 
        (adjoin-term
            (make-term 0 p)
            (the-empty-termlist)
        )
    )
)

(define (mul-poly p1 p2)
    (cond 
        ((same-variable? (variable p1) (variable p2))
            (make-poly (variable p1)
            (mul-terms (term-list p1) (term-list p2)))
        )
        ((variable<? (variable p1) (variable p2)) 
            (mul-poly p1 (canonical (variable p1) p2))
        )
        (else (mul-poly p2 p1))
    )
)

(define (add-poly p1 p2)
    (cond 
        ((same-variable? (variable p1) (variable p2))
            (make-poly (variable p1)
            (add-terms (term-list p1) (term-list p2)))
        )
        ((variable<? (variable p1) (variable p2)) 
            (add-poly p1 (canonical (variable p1) p2))
        )
        (else (add-poly p2 p1))
    )
)

2.93

I replace the natural operations with generic operations. Only when there are integers do make-rat reduce fractions.

(define (make-rat n d)
 (if (and (integer? n) (integer? d))
 	(let ((g (gcd n d)))
 		(if (< (* n d) 0)
    		(cons (- (abs (/ n g))) (abs (/ d g)))
    		(cons (abs (/ n g)) (abs (/ d g)))
 		)
 	)
 	(cons n d)
 )
)

     (define (numer x) (car x)) 
     (define (denom x) (cdr x)) 
     (define (make-rat n d) (cons n d)) 
     (define (add-rat x y) 
         (make-rat (add (mul (numer x) (denom y)) 
                        (mul (numer y) (demom x))) 
                   (mul (denom x) (demom y)))) 
     (define (sub-rat x y) 
         (make-rat (sub (mul (numer x) (denom y)) 
                        (mul (numer y) (demom x))) 
                   (mul (denom x) (demom y)))) 
     (define (mul-rat x y) 
         (make-rat (mul (numer x) (numer y)) 
                   (mul (denom x) (denom y)))) 
     (define (div-rat x y) 
         (make-rat (mul (numer x) (denom y)) 
                   (mul (denom x) (numer y)))) 
      

2.94

You are converting polynomials to new scheme-nums.

Should I be concerned about the different vars?

(define (gcd-terms a b)
  (if (empty-termlist? b)
      a
      (gcd-terms b (remainder-terms a b))))

(define (remainder-terms a b)
	(cadr (div-terms a b))
)

(define (gcd-poly p1 p2)
  (if (same-variable? (variable p1) 
                      (variable p2))
      (make-poly 
       (variable p1)
       (gcd-terms (term-list p1)
                  (term-list p2)))
      (error "Polys not in same var: 
              ADD-POLY"
             (list p1 p2))))

(put 'greatest-common-divisor '(polynomial polynomial) (lambda (a b) (tag (gcd-poly a b))))
(put 'greatest-common-divisor '(scheme-num scheme-num) (lambda (a b) gcd))

Then.

(define (make-rat n d)
 (if (and (integer? n) (integer? d))
 	(let ((g (apply-generic 'greatest-common-divisor a b)))
 		(cons (div n g) (div d g))
 	)
 )
)

2.95

2.96

2.97

I still can’t run all my procedures, cause I don’t have put and get definitions. Maybe I will handle these problems after then.

文档信息

本文作者：nyaaar
本文链接：https://nyaaarlathotep.github.io/2024/10/14/SICP-Exercise-2/
版权声明：自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

SICP Exercise in chapter2

Chapter 2

2.1

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.2

2.17

2.18

2.19

2.20

2.21

2.22

2.23

2.24

2.25

2.26

2.27

2.28

2.29

2.30

2.31

2.32

2.33

2.34

2.35

2.36

2.37

2.38

2.39

2.40

2.41

2.42

2.43

2.44

2.45

2.46

2.47

2.48

2.49

2.50

2.51

2.52

2.53

2.3

2.54

2.55

2.56

2.57

2.58

2.59

2.60

2.61

2.62

2.63

2.64

2.65

2.66

2.67

2.68

2.69

2.70

2.71

2.72

2.4

2.73

2.74

2.75

2.76