笔记
这就全是那种接雨水类型的问题了吧。
91. Eight Queens Problem
This is a classical problem in computer science. The objective is to place eight queens on a chessboard so that no two queens are attacking each other; i.e., no two queens are in the same row, the same column, or on the same diagonal.
Hint: Represent the positions of the queens as a list of numbers 1..N. Example:
[4; 2; 7; 3; 6; 8; 5; 1]means that the queen in the first column is in row 4, the queen in the second column is in row 2, etc. Use the generate-and-test paradigm.# queens_positions 4;; - : int list list = [[3; 1; 4; 2]; [2; 4; 1; 3]]
generate-and-test paradigm,神秘,不用回溯吗?Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking which guarantees to find a solution if done systematically and there exists a solution.哦,要回溯的。
我记得 LeetCode 有个 N 皇后,当时我就不会,这题还不太一样吗,题要 8 皇后,问题是例子里也没有 8 个啊,我就当 N 皇后做了。
let queens_positions max =
let adjacent (ac,ar) (bc,br) =
if (ac-bc) + (ar-br) = 0 || (ac-bc) = (ar-br) || ac = bc || ar = br then true else false
in
let rec aux row column queens =
if row>max then [queens] else
if column > max then [] else
let now = (row, column) in
if any queens (fun q-> adjacent q now) then aux row (column+1) queens else
aux (row+1) 1 (now::queens) @ aux row (column+1) queens
in
List.map (List.map snd) (aux 1 1 [])
少用了内存,没像我把元组存着,导致判定麻烦了点。也差不多。
This is a brute force algorithm enumerating all possible solutions. For a deeper analysis, look for example to Wikipedia.
# let possible row col used_rows usedD1 usedD2 = not (List.mem row used_rows || List.mem (row + col) usedD1 || List.mem (row - col) usedD2) let queens_positions n = let rec aux row col used_rows usedD1 usedD2 = if col > n then [List.rev used_rows] else (if row < n then aux (row + 1) col used_rows usedD1 usedD2 else []) @ (if possible row col used_rows usedD1 usedD2 then aux 1 (col + 1) (row :: used_rows) (row + col :: usedD1) (row - col :: usedD2) else []) in aux 1 1 [] [] [];; val possible : int -> int -> int list -> int list -> int list -> bool = <fun> val queens_positions : int -> int list list = <fun>
92. Knight’s Tour
Another famous problem is this one: How can a knight jump on an N×N chessboard in such a way that it visits every square exactly once?
Hint: Represent the squares by pairs of their coordinates
(x,y), where bothxandyare integers between 1 and N. Define the functionjump n (x,y)that returns all coordinates(u,v)to which a knight can jump from(x,y)to on an×nchessboard. And finally, represent the solution of our problem as a list knight positions (the knight’s tour).
还是国际象棋啊,巧了,最近我也玩了玩国象,线下和小兄弟还玩了玩。有时间可以打打 rank。不用所有可能吗,那还好,这个看起来回溯也会很大。
不多说了,这才叫可读性好吧。
癌,max = 6 的时候就让我的浏览器卡了一会,很恐怖好吧。
let knight_tour max =
let legal_next (x,y) steps=
let right_one = (x+1<=max) in
let right_two = (x+2<=max) in
let left_one = (x-1>=1) in
let left_two = (x-2>=1) in
let down_one = (y+1<=max) in
let down_two = (y+2<=max) in
let up_one = (y-1>=1) in
let up_two = (y-2>=1) in
let res = [] in
let res = if right_one && down_two && (not (List.mem (x+1,y+2) steps))
then (x+1,y+2)::res else res in
let res = if right_two && down_one && (not (List.mem (x+2,y+1) steps))
then (x+2,y+1)::res else res in
let res = if right_one && up_two && (not (List.mem (x+1,y-2) steps))
then (x+1,y-2)::res else res in
let res = if right_two && up_one && (not (List.mem (x+2,y-1) steps))
then (x+2,y-1)::res else res in
let res = if left_one && down_two && (not (List.mem (x-1,y+2) steps))
then (x-1,y+2)::res else res in
let res = if left_two && down_one && (not (List.mem (x-2,y+1) steps))
then (x-2,y+1)::res else res in
let res = if left_one && up_two && (not (List.mem (x-1,y-2) steps))
then (x-1,y-2)::res else res in
let res = if left_two && up_one && (not (List.mem (x-2,y-1) steps))
then (x-2,y-1)::res else res in
res
in
let rec aux now steps = if List.length steps = max*max then Some steps else
let nexts = legal_next now steps in
if List.length nexts = 0 then None else
let rec aaux remain_nexts = match remain_nexts with
| [] -> None
| h::t -> match aux h (h::steps) with
| Some success -> Some success
| None -> aaux t
in
aaux nexts
in
aux (1,1) [(1,1)]
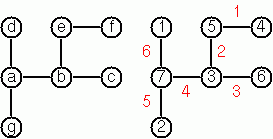
93. Von Koch’s Conjecture
Several years ago I met a mathematician who was intrigued by a problem for which he didn’t know a solution. His name was Von Koch, and I don’t know whether the problem has been solved since.
Anyway, the puzzle goes like this: Given a tree with N nodes (and hence N-1 edges). Find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way, that for each edge K the difference of its node numbers equals to K. The conjecture is that this is always possible.
For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don’t know for sure whether there is always a solution!
Write a function that calculates a numbering scheme for a given tree. What is the solution for the larger tree pictured here?
想起那道图相似的题了,就暴力排列求解呗。哦,这个还不太一样,洗牌的方式比较特别啊。
let rev_concat_map f l = List.fold_left (fun acc x -> List.rev_append (f x) acc) [] l
let (--) l x = List.filter ((<>)x) l
let rec permutation = function
| [] -> []
| x::[] -> [[x]]
| l -> rev_concat_map (fun x -> List.map (fun y -> x::y) (permutation (l--x))) l
let mappings l1 l2 = permutation l2 |> List.map (List.combine l1)
let vk_solution g =
let rec gen_node_num now r= match r with
| [] -> []
| h::t -> now:: (gen_node_num (now+1) t)
in
let node_num = gen_node_num 1 g.nodes in
let possibilities = mappings g.nodes node_num in
let total_edge = List.length g.edges in
let pass map =
let rec check_edge remain_edges edge_nums= match remain_edges with
| [] -> true
| (a,b)::t -> let a_num = List.assoc a map in let b_num = List.assoc b map in
let edge_num = if a_num>b_num then a_num-b_num else b_num-a_num in
if not (List.mem edge_num edge_nums) && edge_num<=total_edge
then check_edge t (edge_num::edge_nums)
else false
in
check_edge g.edges []
in
List.filter (fun e -> pass e) possibilities
我服了,第二个例子果然卡死了,我遭得住啊。第一个例子看着是对的,这种还是得优化。过了吧。
94. An Arithmetic Puzzle (unfinished)
Given a list of integer numbers, find a correct way of inserting arithmetic signs (operators) such that the result is a correct equation. Example: With the list of numbers
[2; 3; 5; 7; 11]we can form the equations 2 - 3 + 5 + 7 = 11 or 2 = (3 * 5 + 7) / 11 (and ten others!).
不是,哥们,这是否有点,Spicy。
生成了好多,好多那种两个 list 互相结合衍生一堆小的那种情况,哇,好麻烦。
let find_equation l =
let make_success left right =
in
let rec eval_poss list =
match list with
| [] -> raise Not_found
| [h] -> [(h, [(string_of_int h)])]
| [a;b] ->
let a_str = string_of_int a in
let b_str = string_of_int b in
[(a+b, ["(";a_str;"+";b_str;")"]); (a-b,["(";a_str;"+";b_str;")"]);
(a*b,["(";a_str;"+";b_str;")"]); (a/b,["(";a_str;"+";b_str;")"])]
| a::b::t -> let l1 = [(a+b, ["(";a_str;"+";b_str;")"]); (a-b,["(";a_str;"+";b_str;")"]);
(a*b,["(";a_str;"+";b_str;")"]); (a/b,["(";a_str;"+";b_str;")"])] in
let l2 = eval_poss t in
List.fold_left (
fun acc (l2ea,l2eb) ->
let l2e_str = string_of_int l2eb in
List.fold_left (fun inner_acc (l1ea,l1eb) ->
let l1e_str = string_of_int l1eb in
[(l1ea+l2eb, ["(";l1e_str;"+";l2e_str;")"]); (l1ea-l2eb,["(";l1e_str;"+";l2e_str;")"]);
(l1ea*l2eb,["(";l1e_str;"+";l2e_str;")"]); (l1ea/l2eb,["(";l1e_str;"+";l2e_str;")"])]
@ inner_acc
) acc l1
) [] l2
in
let rec make_more remain left success = match remain with
| [] -> raise Not_found
| [e] -> success
| h::t -> let left = h::left in
make_more t left (success @ make_success left t)
in
make_more l [] []
I can’t afford it any more. Just gone.
95. English Number Words
On financial documents, like cheques, numbers must sometimes be written in full words. Example: 175 must be written as one-seven-five. Write a function
full_wordsto print (non-negative) integer numbers in full words.# full_words 175;; - : string = "one-seven-five"
let rec full_words n =
let table = [(0,"zero");(1,"one");(2,"two");(3,"three");(4,"four");(5,"five");(6,"six");(7,"seven");(8,"eight");(9,"nine")] in
let rec aux num =
if num = 0 then [] else
let last_num = num mod 10 in
List.assoc last_num table :: aux ((num-last_num)/10)
in
let rec rev_join words splitor = match words with
| [] -> ""
| [h] -> h
| h::t -> rev_join t splitor ^ splitor ^ h
in
rev_join (aux n) "-";;
val full_words : int -> string = <fun>
brilliant! There sure is array list in OCaml.
# let full_words = let digit = [|"zero"; "one"; "two"; "three"; "four"; "five"; "six"; "seven"; "eight"; "nine"|] in let rec words w n = if n = 0 then (match w with [] -> [digit.(0)] | _ -> w) else words (digit.(n mod 10) :: w) (n / 10) in fun n -> String.concat "-" (words [] n);; val full_words : int -> string = <fun>
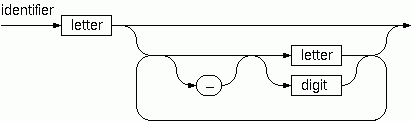
96. Syntax Checker
In a certain programming language (Ada) identifiers are defined by the syntax diagram (railroad chart) opposite. Transform the syntax diagram into a system of syntax diagrams which do not contain loops; i.e. which are purely recursive. Using these modified diagrams, write a function
identifier : string -> boolthat can check whether or not a given string is a legal identifier.# identifier "this-is-a-long-identifier";; - : bool = true
It looks like regex.
let identifier exp =
let letter c = 'a' <= c && c <= 'z' in
let num_or_letter c = letter c || ('0' <= c && c <= '9') in
let len = String.length exp in
if len = 0 then false else
let rec other_word index underscore=
if index >= len then true else
if exp.[index] = '-' && not underscore then false else
if exp.[index] = '-' then other_word (index+1) false else
if num_or_letter exp.[index] then other_word (index+1) true else false
in
let rec start_word index underscore=
if index >= len then true else
if exp.[index] = '-' && not underscore then false else
if exp.[index] = '-' then other_word index false else
if letter exp.[index] then other_word (index+1) true else false
in
start_word 0 false
Zero length string is alse false.
# let identifier = let is_letter c = 'a' <= c && c <= 'z' in let is_letter_or_digit c = is_letter c || ('0' <= c && c <= '9') in let rec is_valid s i not_after_dash = if i < 0 then not_after_dash else if is_letter_or_digit s.[i] then is_valid s (i - 1) true else if s.[i] = '-' && not_after_dash then is_valid s (i - 1) false else false in fun s -> ( let n = String.length s in n > 0 && is_letter s.[n - 1] && is_valid s (n - 2) true);; val identifier : string -> bool = <fun>
97. Sudoku
Sudoku puzzles go like this:
Problem statement Solution . . 4 | 8 . . | . 1 7 9 3 4 | 8 2 5 | 6 1 7 | | | | 6 7 . | 9 . . | . . . 6 7 2 | 9 1 4 | 8 5 3 | | | | 5 . 8 | . 3 . | . . 4 5 1 8 | 6 3 7 | 9 2 4 --------+---------+-------- --------+---------+-------- 3 . . | 7 4 . | 1 . . 3 2 5 | 7 4 8 | 1 6 9 | | | | . 6 9 | . . . | 7 8 . 4 6 9 | 1 5 3 | 7 8 2 | | | | . . 1 | . 6 9 | . . 5 7 8 1 | 2 6 9 | 4 3 5 --------+---------+-------- --------+---------+-------- 1 . . | . 8 . | 3 . 6 1 9 7 | 5 8 2 | 3 4 6 | | | | . . . | . . 6 | . 9 1 8 5 3 | 4 7 6 | 2 9 1 | | | | 2 4 . | . . 1 | 5 . . 2 4 6 | 3 9 1 | 5 7 8Every spot in the puzzle belongs to a (horizontal) row and a (vertical) column, as well as to one single 3x3 square (which we call “square” for short). At the beginning, some of the spots carry a single-digit number between 1 and 9. The problem is to fill the missing spots with digits in such a way that every number between 1 and 9 appears exactly once in each row, in each column, and in each square.
# (* The board representation is not imposed. Here "0" stands for "." *);;
How could I input the board? Gross.
Nevermind. It’s about time using some brute forces resorts.
98. Nonograms
Around 1994, a certain kind of puzzles was very popular in England. The “Sunday Telegraph” newspaper wrote: “Nonograms are puzzles from Japan and are currently published each week only in The Sunday Telegraph. Simply use your logic and skill to complete the grid and reveal a picture or diagram.” As an OCaml programmer, you are in a better situation: you can have your computer do the work!
The puzzle goes like this: Essentially, each row and column of a rectangular bitmap is annotated with the respective lengths of its distinct strings of occupied cells. The person who solves the puzzle must complete the bitmap given only these lengths.
Problem statement: Solution: |_|_|_|_|_|_|_|_| 3 |_|X|X|X|_|_|_|_| 3 |_|_|_|_|_|_|_|_| 2 1 |X|X|_|X|_|_|_|_| 2 1 |_|_|_|_|_|_|_|_| 3 2 |_|X|X|X|_|_|X|X| 3 2 |_|_|_|_|_|_|_|_| 2 2 |_|_|X|X|_|_|X|X| 2 2 |_|_|_|_|_|_|_|_| 6 |_|_|X|X|X|X|X|X| 6 |_|_|_|_|_|_|_|_| 1 5 |X|_|X|X|X|X|X|_| 1 5 |_|_|_|_|_|_|_|_| 6 |X|X|X|X|X|X|_|_| 6 |_|_|_|_|_|_|_|_| 1 |_|_|_|_|X|_|_|_| 1 |_|_|_|_|_|_|_|_| 2 |_|_|_|X|X|_|_|_| 2 1 3 1 7 5 3 4 3 1 3 1 7 5 3 4 3 2 1 5 1 2 1 5 1For the example above, the problem can be stated as the two lists
[[3]; [2; 1]; [3; 2]; [2; 2]; [6]; [1; 5]; [6]; [1]; [2]]and[[1; 2]; [3; 1]; [1; 5]; [7; 1]; [5]; [3]; [4]; [3]]which give the “solid” lengths of the rows and columns, top-to-bottom and left-to-right, respectively. Published puzzles are larger than this example, e.g. 25×20, and apparently always have unique solutions.# solve [[3]; [2; 1]; [3; 2]; [2; 2]; [6]; [1; 5]; [6]; [1]; [2]] [[1; 2]; [3; 1]; [1; 5]; [7; 1]; [5]; [3]; [4]; [3]];;
It seems familiar.
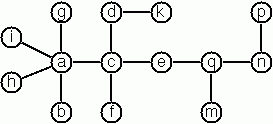
99. Crossword Puzzle
Given an empty (or almost empty) framework of a crossword puzzle and a set of words. The problem is to place the words into the framework.
The particular crossword puzzle is specified in a text file which first lists the words (one word per line) in an arbitrary order. Then, after an empty line, the crossword framework is defined. In this framework specification, an empty character location is represented by a dot (.). In order to make the solution easier, character locations can also contain predefined character values. The puzzle above is defined in the file p7_09a.dat, other examples are p7_09b.dat and p7_09d.dat. There is also an example of a puzzle (p7_09c.dat) which does not have a solution.
Words are strings (character lists) of at least two characters. A horizontal or vertical sequence of character places in the crossword puzzle framework is called a site. Our problem is to find a compatible way of placing words onto sites.
Hints:
- The problem is not easy. You will need some time to thoroughly understand it. So, don’t give up too early! And remember that the objective is a clean solution, not just a quick-and-dirty hack!
- For efficiency reasons it is important, at least for larger puzzles, to sort the words and the sites in a particular order.
Lol, spending time doesn’t make me understand.
100. Never-Ending Sequences
Lists are finite, meaning they always contain a finite number of elements. Sequences may be finite or infinite.
The goal of this exercise is to define a type
'a streamwhich only contains infinite sequences. Using this type, define the following functions:val hd : 'a stream -> 'a (** Returns the first element of a stream *) val tl : 'a stream -> 'a stream (** Removes the first element of a stream *) val take : int -> 'a stream -> 'a list (** [take n seq] returns the n first values of [seq] *) val unfold : ('a -> 'b * 'a) -> 'a -> 'b stream (** Similar to Seq.unfold *) val bang : 'a -> 'a stream (** [bang x] produces an infinitely repeating sequence of [x] values. *) val ints : int -> int stream (* Similar to Seq.ints *) val map : ('a -> 'b) -> 'a stream -> 'b stream (** Similar to List.map and Seq.map *) val filter: ('a -> bool) -> 'a stream -> 'a stream (** Similar to List.filter and Seq.filter *) val iter : ('a -> unit) -> 'a stream -> 'b (** Similar to List.iter and Seq.iter *) val to_seq : 'a stream -> 'a Seq.t (** Translates an ['a stream] into an ['a Seq.t] *) val of_seq : 'a Seq.t -> 'a stream (** Translates an ['a Seq.t] into an ['a stream] @raise Failure if the input sequence is finite. *)Tip: Use
let ... =patterns.
Oh, finally there’s another beginner level problem.
I don’t get it. I even can’t understand the solution…
I kinda get it, it’s like Y combinator or something? the function passed as paramter won’t excuted till it’s been called. The infinite comes from here.
The key function is unfold. It use a empty tuple as a placeholder to prevent the function from executing.
type 'a cons = Cons of 'a * 'a stream and 'a stream = unit -> 'a cons let hd (seq : 'a stream) = let (Cons (x, _)) = seq () in x let tl (seq : 'a stream) = let (Cons (_, seq)) = seq () in seq let rec take n seq = if n = 0 then [] else let (Cons (x, seq)) = seq () in x :: take (n - 1) seq let rec unfold f x () = let (y, x) = f x in Cons (y, unfold f x) let bang x = unfold (fun x -> (x, x)) x let ints x = unfold (fun x -> (x, x + 1)) x let rec map f seq () = let (Cons (x, seq)) = seq () in Cons (f x, map f seq) let rec filter p seq () = let (Cons (x, seq)) = seq () in let seq = filter p seq in if p x then Cons (x, seq) else seq () let rec iter f seq = let (Cons (x, seq)) = seq () in f x; iter f seq let to_seq seq = Seq.unfold (fun seq -> Some (hd seq, tl seq)) seq let rec of_seq seq () = match seq () with | Seq.Nil -> failwith "Not a infinite sequence" | Seq.Cons (x, seq) -> Cons (x, of_seq seq)
101. Diagonal of a Sequence of Sequences
Write a function
diag : 'a Seq.t Seq.t -> 'a Seqthat returns the diagonal of a sequence of sequences. The returned sequence is formed as follows: The first element of the returned sequence is the first element of the first sequence; the second element of the returned sequence is the second element of the second sequence; the third element of the returned sequence is the third element of the third sequence; and so on.
It seems like the test to the problem above.
The question is I don’t know much about Seq. Nevermind. I will check the doc again.
Oh, Seq has its own fold.
let diag all =
let rec take_nth n seq = match seq with
| Seq.Nil -> None
| Seq.Cons (h,t) -> if n=0 then Some h else take_nth (n-1) (t ())
in
Seq.unfold (fun (seq, index) -> match seq with
| Seq.Nil -> None
| Seq.Cons (h,t) -> let x = take_nth index h in
Some (x ,(t (), (index+1)))
) (all, 0);;
val diag : 'a Seq.node Seq.node -> 'a option Seq.t = <fun>
bravo!
I don’t get it, again. Man!
let rec diag seq_seq () = let hds, tls = Seq.filter_map Seq.uncons seq_seq |> Seq.split in let hd, tl = Seq.uncons hds |> Option.map fst, Seq.uncons tls |> Option.map snd in let d = Option.fold ~none:Seq.empty ~some:diag tl in Option.fold ~none:Fun.id ~some:Seq.cons hd d ()
总结
结束了,还有一些遗留的问题,找时间扫下尾。做了我两个月,痛苦好吧。虽然叫 99 problems 但是却有 101 道,而且里面还有好多一道分两个 A,B 的,呃呃。
OCaml 确实有点东西,这个函数式的巧妙运用和场景可以找时间总结下。
2024.11.23
巧了,我当时写到的时候,就觉得这种运用将函数转化为闭包的形式从而将一些操作延迟执行的方法肯定大有所为,简化很多操作,同时还有丰富的表达能力。但一时又找不到什么特殊场景不得不这么做。后面在 SICP 第三章学到最后一部分的 stream,和这里的 stream 是同一种概念的延迟执行的 sequence。SICP 里有这种场景:两个函数互相依赖,但又只依赖对方的前一个元素来生成下一个元素,此时只有这种写法可以定义这样的函数。
这样的延迟执行还有许多优势,仔细学习后感觉确实强大。
文档信息
- 本文作者:nyaaar
- 本文链接:https://nyaaarlathotep.github.io/2024/09/13/Ocaml-99-%E9%97%AE%E9%A2%98%E7%AC%94%E8%AE%B0-7/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)