笔记
80. Conversions
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of different nodes.
There are several ways to represent graphs in OCaml.
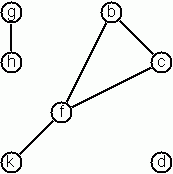
- One method is to list all edges, an edge being a pair of nodes. In this form, the graph depicted opposite is represented as the following expression:
# [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')];; - : (char * char) list = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]We call this edge-clause form. Obviously, isolated nodes cannot be represented.
- Another method is to represent the whole graph as one data object. According to the definition of the graph as a pair of two sets (nodes and edges), we may use the following OCaml type:
# type 'a graph_term = {nodes : 'a list; edges : ('a * 'a) list};; type 'a graph_term = { nodes : 'a list; edges : ('a * 'a) list; }Then, the above example graph is represented by:
# let example_graph = {nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k']; edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]};; val example_graph : char graph_term = {nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k']; edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]}We call this graph-term form. Note, that the lists are kept sorted, they are really sets, without duplicated elements. Each edge appears only once in the edge list; i.e. an edge from a node x to another node y is represented as
(x, y), the couple(y, x)is not present. The graph-term form is our default representation. You may want to define a similar type using sets instead of lists.
- A third representation method is to associate with each node the set of nodes that are adjacent to that node. We call this the adjacency-list form. In our example:
(* example pending *)
- The representations we introduced so far well suited for automated processing, but their syntax is not very user-friendly. Typing the terms by hand is cumbersome and error-prone. We can define a more compact and “human-friendly” notation as follows: A graph (with char labelled nodes) is represented by a string of atoms and terms of the type X-Y. The atoms stand for isolated nodes, the X-Y terms describe edges. If an X appears as an endpoint of an edge, it is automatically defined as a node. Our example could be written as:
# "b-c f-c g-h d f-b k-f h-g";; - : string = "b-c f-c g-h d f-b k-f h-g"We call this the human-friendly form. As the example shows, the list does not have to be sorted and may even contain the same edge multiple times. Notice the isolated node
d.Write functions to convert between the different graph representations. With these functions, all representations are equivalent; i.e. for the following problems you can always pick freely the most convenient form. This problem is not particularly difficult, but it’s a lot of work to deal with all the special cases.
adjacency-list form定义都没给我怎么转化啊。
let human_to_graph s= let h_edges = String.split_on_char ' ' s in
let add_node node ns =
if not (List.exists (fun e -> e = node) ns)
then node::ns else ns
in
let rec aux l ns es= match l with
| [] -> {nodes = ns;edges = es}
| p::t ->
let (ns,es) = if String.length p = 1 then(add_node p.[0] ns, es)
else
let ns = add_node p.[0] ns in
let ns = add_node p.[2] ns in
let es = if not (List.exists (fun e -> e=(p.[0], p.[2])) es)
then (p.[0], p.[2])::es else es in
(ns, es) in
aux t ns es
in
aux h_edges [] []
又没答案。
81. Path From One Node to Another One
Write a function
paths g a bthat returns all acyclic pathpfrom nodeato nodeb ≠ ain the graphg. The function should return the list of all paths via backtracking.# let example_graph = {nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k']; edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]};; val example_graph : char graph_term = {nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k']; edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]} # paths example_graph 'f' 'b';; - : char list list = [['f'; 'c'; 'b']; ['f'; 'b']]
感觉得写一些通用的图的方法。比如 list.contain 这种的,有无环判断真的很麻烦。
有预感又要死循环了,很痛苦。
很多地方可以用 Option 改良一下,能好看很多。癌,差不多得了。
let paths g start end_node =
let nodes,edges = g.nodes, g.edges in
let rec find_to s edges = match edges with
| [] -> []
| (from, next)::t -> if from = s then next::find_to s t
else if next = s then from::find_to s t
else find_to s t
in
let rec valid_next path ns = match ns with
| [] -> []
| h::t -> if (List.exists (fun e-> e=h) path) then (valid_next path t) else h::(valid_next path t)
in
let rec aux path now =
let next_nodes = valid_next path (find_to now edges) in
let goals = List.map (fun e -> e::path) (List.filter (fun e -> e = end_node) next_nodes) in
let others = List.filter (fun e -> e != end_node) next_nodes in
List.fold_left (fun n t-> n @ (aux (t::path) t)) goals others
in
List.map (fun e-> List.rev e) (aux [start] start);;
这个 neighbors 写的就比我的 find_to 要好,还能把去环逻辑下压到这个函数里完成了,挺好的,有点像 Graph.filter 了。
List.mem 就是 List.contain 哦。
妙啊,它其实是从 b 走到 a 的,这样就不用 List.rev 了。这个递归也做的比我优雅多了,强啊,递归出来是个 list list,又被 concat_map 打平。
# (* The datastructures used here are far from the most efficient ones but allow for a straightforward implementation. *) (* Returns all neighbors satisfying the condition. *) let neighbors g a cond = let edge l (b, c) = if b = a && cond c then c :: l else if c = a && cond b then b :: l else l in List.fold_left edge [] g.edges let rec list_path g a to_b = match to_b with | [] -> assert false (* [to_b] contains the path to [b]. *) | a' :: _ -> if a' = a then [to_b] else let n = neighbors g a' (fun c -> not (List.mem c to_b)) in List.concat_map (fun c -> list_path g a (c :: to_b)) n let paths g a b = assert(a <> b); list_path g a [b];; val neighbors : 'a graph_term -> 'a -> ('a -> bool) -> 'a list = <fun> val list_path : 'a graph_term -> 'a -> 'a list -> 'a list list = <fun> val paths : 'a graph_term -> 'a -> 'a -> 'a list list = <fun>
82. Cycle From a Given Node
Write a functions
cycle g athat returns a closed path (cycle)pstarting at a given nodeain the graphg. The predicate should return the list of all cycles via backtracking.# let example_graph = {nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k']; edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]};; val example_graph : char graph_term = {nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k']; edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]} # cycles example_graph 'f';; - : char list list = [['f'; 'b'; 'c'; 'f']; ['f'; 'c'; 'f']; ['f'; 'c'; 'b'; 'f']; ['f'; 'b'; 'f']; ['f'; 'k'; 'f']]
偷一手上一道题的 neighbors 好吧。
let neighbors g a cond =
let edge l (b, c) = if b = a && cond c then c :: l
else if c = a && cond b then b :: l
else l in
List.fold_left edge [] g.edges;;
val neighbors : 'a graph_term -> 'a -> ('a -> bool) -> 'a list = <fun>
let cycles g start =
let rec list_path g to_b = match to_b with
| [] -> assert false (* [to_b] contains the path to [b]. *)
| a' :: t ->if a' = start && List.length to_b!=1 then [to_b]
else
let n = neighbors g a' (fun c -> c=start || (not (List.mem c to_b))) in
List.concat_map (fun c -> list_path g (c :: to_b)) n
in
list_path g [start];;
val cycles : 'a graph_term -> 'a -> 'a list list = <fun>
强啊,这个思路。
# let cycles g a = let n = neighbors g a (fun _ -> true) in let p = List.concat_map (fun c -> list_path g a [c]) n in List.map (fun p -> p @ [a]) p;; val cycles : 'a graph_term -> 'a -> 'a list list = <fun>
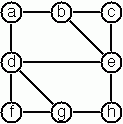
83. Construct All Spanning Trees
Write a function
s_tree gto construct (by backtracking) all spanning trees of a given graphg. With this predicate, find out how many spanning trees there are for the graph depicted to the left. The data of this example graph can be found in the test below. When you have a correct solution for thes_treefunction, use it to define two other useful functions:is_tree graphandis_connected Graph. Both are five-minutes tasks!# let g = {nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h']; edges = [('a', 'b'); ('a', 'd'); ('b', 'c'); ('b', 'e'); ('c', 'e'); ('d', 'e'); ('d', 'f'); ('d', 'g'); ('e', 'h'); ('f', 'g'); ('g', 'h')]};; val g : char graph_term = {nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h']; edges = [('a', 'b'); ('a', 'd'); ('b', 'c'); ('b', 'e'); ('c', 'e'); ('d', 'e'); ('d', 'f'); ('d', 'g'); ('e', 'h'); ('f', 'g'); ('g', 'h')]}
生成树吗,都是搞最小生成树的,结果你来个生成树,又得想个方法怎么好去重了。
哦,好像也不用去重,不需要多节点出发的,单节点就能获得所有结果了。
let s_tree g =
let rec aux used_nodes edges now = if List.length used_nodes = List.length g.nodes then [{nodes = used_nodes; edges = edges}] else
let next_nodes = neighbors g now (fun e -> not (List.mem e used_nodes)) in
let rec go_next remain = match remain with
| [] -> []
| h::t -> (aux (h::used_nodes) ((h,now)::edges) h) @ go_next t
in
go_next next_nodes
in
match g.nodes with
| []-> raise Not_found
| h::t -> aux [h] [] h
let is_tree g = if List.length (s_tree g) = 1 then true else false
let is_connected g = if List.length (s_tree g) = 0 then false else false
癌,我服了,又没答案。
稍微盯了一下,感觉应该是全的。
84. Construct the Minimal Spanning Tree
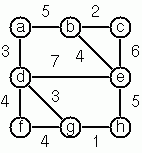
Write a function
ms_tree graphto construct the minimal spanning tree of a given labelled graph. A labelled graph will be represented as follows:# type ('a, 'b) labeled_graph = {nodes : 'a list; labeled_edges : ('a * 'a * 'b) list};; type ('a, 'b) labeled_graph = { nodes : 'a list; labeled_edges : ('a * 'a * 'b) list; }(Beware that from now on
nodesandedgesmask the previous fields of the same name.)Hint: Use the algorithm of Prim. A small modification of the solution of P83 does the trick. The data of the example graph to the right can be found below.
# let g = {nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h']; labeled_edges = [('a', 'b', 5); ('a', 'd', 3); ('b', 'c', 2); ('b', 'e', 4); ('c', 'e', 6); ('d', 'e', 7); ('d', 'f', 4); ('d', 'g', 3); ('e', 'h', 5); ('f', 'g', 4); ('g', 'h', 1)]};; val g : (char, int) labeled_graph = {nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h']; labeled_edges = [('a', 'b', 5); ('a', 'd', 3); ('b', 'c', 2); ('b', 'e', 4); ('c', 'e', 6); ('d', 'e', 7); ('d', 'f', 4); ('d', 'g', 3); ('e', 'h', 5); ('f', 'g', 4); ('g', 'h', 1)]}
你来了,复习一遍 Prim 好吧。
这个 closest_neighbor 也应该用 option 搞一下的,懒得搞了,硬编码了个 1000 作为最大值,很丑陋。
let closest_neighbor g node_list =
let edge (next,(b', c', min_len)) (b, c, len) =
if (List.mem b node_list) && not (List.mem c node_list) && (len<min_len) then (c,(b, c, len))
else if (List.mem c node_list) && not (List.mem b node_list) && (len<min_len) then (b,(b, c, len))
else (next, (b', c', min_len)) in
List.fold_left edge ('a',('a','a', 1000)) g.labeled_edges;;
let ms_tree g =
let rec aux new_tree = if List.length new_tree.nodes = List.length g.nodes then new_tree else
let (next, edge) = closest_neighbor g new_tree.nodes in
aux {nodes = next::new_tree.nodes; labeled_edges = edge::new_tree.labeled_edges}
in
match g.nodes with
| []-> raise Not_found
| h::t -> aux {nodes= [h]; labeled_edges = []}
咋回事?又没答案。
看了眼后面的好多没答案啊,什么情况,要靠自己了吗?
85. Graph Isomorphism
Two graphs G1(N1,E1) and G2(N2,E2) are isomorphic if there is a bijection f: N1 → N2 such that for any nodes X,Y of N1, X and Y are adjacent if and only if f(X) and f(Y) are adjacent.
Write a function that determines whether two graphs are isomorphic.
Hint: Use an open-ended list to represent the function f.
# let g = {nodes = [1; 2; 3; 4; 5; 6; 7; 8]; edges = [(1, 5); (1, 6); (1, 7); (2, 5); (2, 6); (2, 8); (3, 5); (3, 7); (3, 8); (4, 6); (4, 7); (4, 8)]};; val g : int graph_term = {nodes = [1; 2; 3; 4; 5; 6; 7; 8]; edges = [(1, 5); (1, 6); (1, 7); (2, 5); (2, 6); (2, 8); (3, 5); (3, 7); (3, 8); (4, 6); (4, 7); (4, 8)]}
额啊,图相似,我记得这个还有个什么特殊的算法来着。
查了查没太找到,要不直接暴力得了。
不行了,太麻烦了,想要稍微剪枝一下都要很麻烦的回溯和递归,还是暴力搞吧。
暴力也得回溯,也挺麻烦的。
let graphg_iso g1 g2 =
if List.length g1.nodes != List.length g2.nodes || List.length g1.edges != List.length g2.nodes then false
else
let rec remove e l = match l with
| []->[]
| h::t -> if h = e then t else h::remove e t
in
let rec shuffle remain_a remain_b =
if List.length remain_a = 0 then [[]] else
let first = List.fold_left
(fun l1 t1-> List.fold_left (fun l2 t2 ->(t1,t2)::l2) l1 remain_b) [] remain_a in
List.flatten (List.map
(fun (t1,t2) ->
let tails= shuffle (remove t1 remain_a) (remove t2 remain_b) in
List.map (fun e-> (t1,t2)::e) tails )
first)
in
let rec any l f = match l with
| [] -> false
| h::t -> if f h then true else any t f
in
let make_more_maps a a_neis b b_neis map =
let rec get_unmap_neis remain_a remain_b last= match last with
| [] -> ((remain_a,remain_b),true)
| h::t -> match List.assoc_opt h map with
| Some(h_mapped_b) -> if List.mem h_mapped_b b_neis then
get_unmap_neis (remove h remain_a) (remove h_mapped_b remain_b) t
else (([],[]),false)
| None -> get_unmap_neis remain_a remain_b t
in
let ((remain_a,remain_b,succ) = get_unmap_neis a_neis b_neis a_neis in
if !succ then false
else
let other_map = shuffle remain_a remain_b in
List.map (fun e-> map @ e) other_map
in
let rec legal a a_neis map remain_g1_nodes remain_g2_nodes=
let rec find_legal_b g2_nodes= match g2_nodes with
| [] -> false
| h::t -> let h_neis = neighbors h in
if List.length h_neis != a_neis then find_legal_b t
else
in
match List.assoc_opt a map with
| Some(b) -> match_g1 remain_g1_nodes remain_g2_nodes map
| None -> find_legal_b remain_g2_nodes
in
let rec match_g1 remain_g1_nodes remain_g2_nodes map =
match remain_g1_nodes with
| [] -> true
| h::t -> let h_neighbors = neighbors h in
太复杂了,分步测试 一下。get_unmap_neis这一步是为了把两个选定的点的边从已经存在的映射关系中验证并去除,返回(char list * char list) * bool,第二个 bool 是这种情况是否合法,第一个元素(char list * char list)是可以随意搭配产生 map 的点。
这些都是为了下一步产生当前状况下可能存在的 map。
其实应该拆分成两个函数的。
let make_more_maps a a_neis b b_neis map =
let rec get_unmap_neis remain_a remain_b last= match last with
| [] -> ((remain_a,remain_b),true)
| h::t -> match List.assoc_opt h map with
| Some(h_mapped_b) -> if List.mem h_mapped_b b_neis then
get_unmap_neis (remove h remain_a) (remove h_mapped_b remain_b) t
else (([],[]),false)
| None -> get_unmap_neis remain_a remain_b t
in
get_unmap_neis a_neis b_neis a_neis
shuffle 生成可能存在的 map 关系,但问题是数量级是 n^2*(n-1)^2…,很恐怖好吧。
哦,我还没去重,我真的是。。。
let rec shuffle remain_a remain_b =
if List.length remain_a = 0 then [[]] else
let first = List.fold_left
(fun l1 t1-> List.fold_left (fun l2 t2 ->(t1,t2)::l2) l1 remain_b) [] remain_a in
List.flatten (List.map
(fun (t1,t2) ->
let tails= shuffle (remove t1 remain_a) (remove t2 remain_b) in
List.map (fun e-> (t1,t2)::e) tails )
first)
癌,我选择死亡。写不出来了。
let rev_concat_map f l = List.fold_left (fun acc x -> List.rev_append (f x) acc) [] l let (--) l x = List.filter ((<>)x) l let rec permutation = function | [] -> [] | x::[] -> [[x]] | l -> rev_concat_map (fun x -> List.map (fun y -> x::y) (permutation (l--x))) l let mappings l1 l2 = permutation l2 |> List.map (List.combine l1) let f mapping x = List.assoc x mapping let is_isomorphism g1 g2 = if List.length g1.nodes = List.length g2.nodes && List.length g1.edges = List.length g2.edges then let ms = mappings g1.nodes g2.nodes in let test m (a,b) es2 = List.mem (f m a, f m b) es2 || List.mem (f m b, f m a) es2 in let rec test_all m es2 = function | [] -> true | e::es1 -> test m e es2 && test_all m es2 es1 in let rec test_all_mappings = function | [] -> false | m::ms -> test_all m g2.edges g1.edges || test_all_mappings ms in test_all_mappings ms else false
哦,这直接把所有节点排列组合了,再验证是否合法,你比我还暴力。
mappings 就是我的 shuffle,你是怎么做到的?哎,牛逼,把 a2 打乱的所有可能,再和 a1 List.combine,也就不用去重了,根本不用每一个元素去生成所有可能的对应的情况再加上自己。
| > 这个是 pipe 操作符啊。 |
86. Node Degree and Graph Coloration
- Write a function
degree graph nodethat determines the degree of a given node.- Write a function that generates a list of all nodes of a graph sorted according to decreasing degree.
- Use Welsh-Powell’s algorithm to paint the nodes of a graph in such a way that adjacent nodes have different colors.
let neighbors g a =
let edge l (b, c) = if b = a then c :: l
else if c = a then b :: l
else l in
List.fold_left edge [] g.edges;;
val neighbors : 'a graph_term -> 'a -> 'a list = <fun>
let degree g node = List.length (neighbors g node);;
val degree : 'a graph_term -> 'a -> int = <fun>
let sort_node_degree g = List.map (fun e-> fst e) (List.sort (fun (a,a_d) (b,b_d) -> b_d-a_d)
(List.map (fun e -> (e, degree g e)) g.nodes))
let paint g = let nodes = sort_node_degree g in
let rec aux color remain = match remain with
| [] -> []
| h::t -> let h_nei = neighbors g h in
let colored = ((h, color):: aux color (List.filter (fun e -> not (List.mem e h_nei)) t)) in
colored @ (aux (color+1) (
List.filter (fun e -> not (List.mem_assoc e colored)) t
))
in
aux 1 nodes
这个版本还有点问题,去除已经涂了的节点导致一些相邻的节点变得不相邻了,得改下,呃呃。
癌,我真是服了,de 了半天,List.mem_assoc 这个有点问题,没玩明白,和我预期的不一样,盯着看了半天。吐了,花了好多时间。
let paint g = let nodes = sort_node_degree g in
let rec aux color remain = match remain with
| [] -> []
| h::t -> let h_nei = neighbors g h in
let colored = ((h, color):: aux color (List.filter (fun e -> not (List.mem e h_nei)) t)) in
let colored_nodes = List.map fst colored in
colored @ (aux (color+1) (
List.filter (fun e -> not (List.mem e colored_nodes)) t
))
in
aux 1 nodes
87. Depth-First Order Graph Traversal
Write a function that generates a depth-first order graph traversal sequence. The starting point should be specified, and the output should be a list of nodes that are reachable from this starting point (in depth-first order).
Specifically, the graph will be provided by its adjacency-list representation and you must create a module
Mwith the following signature:# module type GRAPH = sig type node = char type t val of_adjacency : (node * node list) list -> t val dfs_fold : t -> node -> ('a -> node -> 'a) -> 'a -> 'a end;; module type GRAPH = sig type node = char type t val of_adjacency : (node * node list) list -> t val dfs_fold : t -> node -> ('a -> node -> 'a) -> 'a -> 'a endwhere
M.dfs_fold g n f aappliesfon the nodes of the graphgin depth first order, starting with noden.# let g = M.of_adjacency ['u', ['v'; 'x']; 'v', ['y']; 'w', ['z'; 'y']; 'x', ['v']; 'y', ['x']; 'z', ['z']; ];; val g : M.t = <abstr>
什么意思哦,还得自己写一个 module,要瞧一瞧了。
module M : GRAPH = struct
module Char_map = Map.Make (Char)
type node = char
type t = (node list) Char_map.t
;;
let of_adjacency l =
List.fold_left (fun acc (s, ends) -> Char_map.add s ends acc) Char_map.empty l;;
let dfs_fold g c fn acc = let module CSet=Set.Make(Char) in
let rec aux visited now aux_acc =
if CSet.mem now visited then (aux_acc,visited) else
let new_visited = CSet.add now visited in
let new_acc = fn aux_acc now in
let next_nodes = Char_map.find now g in
List.fold_left
(fun (son_acc,next_visited) next_node -> aux next_visited next_node son_acc)
(new_acc,new_visited) next_nodes
in
aux (CSet.empty) c acc |>fst
end;;
module M : GRAPH
题里面给的例子居然是不联通的。。。很神秘。
应该能搞一个用 Functor 做成多种类型都能塞的图的,OCaml 这个 module 签名系统还满神秘的,有点像接口。
In a depth-first search you fully explore the edges of the most recently discovered node v before ‘backtracking’ to explore edges leaving the node from which v was discovered. To do a depth-first search means keeping careful track of what vertices have been visited and when.
We compute timestamps for each vertex discovered in the search. A discovered vertex has two timestamps associated with it : its discovery time (in map
d) and its finishing time (in mapf) (a vertex is finished when its adjacency list has been completely examined). These timestamps are often useful in graph algorithms and aid in reasoning about the behavior of depth-first search.We color nodes during the search to help in the bookkeeping (map
color). All vertices of the graph are initiallyWhite. When a vertex is discovered it is markedGrayand when it is finished, it is markedBlack.If vertex v is discovered in the adjacency list of previously discovered node u, this fact is recorded in the predecessor subgraph (map
pred).# module M : GRAPH = struct module Char_map = Map.Make (Char) type node = char type t = (node list) Char_map.t let of_adjacency l = List.fold_right (fun (x, y) -> Char_map.add x y) l Char_map.empty type colors = White|Gray|Black type 'a state = { d : int Char_map.t; (*discovery time*) f : int Char_map.t; (*finishing time*) pred : char Char_map.t; (*predecessor*) color : colors Char_map.t; (*vertex colors*) acc : 'a; (*user specified type used by 'fold'*) } let dfs_fold g c fn acc = let rec dfs_visit t u {d; f; pred; color; acc} = let edge (t, state) v = if Char_map.find v state.color = White then dfs_visit t v {state with pred = Char_map.add v u state.pred} else (t, state) in let t, {d; f; pred; color; acc} = let t = t + 1 in List.fold_left edge (t, {d = Char_map.add u t d; f; pred; color = Char_map.add u Gray color; acc = fn acc u}) (Char_map.find u g) in let t = t + 1 in t , {d; f = Char_map.add u t f; pred; color = Char_map.add u Black color; acc} in let v = List.fold_left (fun k (x, _) -> x :: k) [] (Char_map.bindings g) in let initial_state= {d = Char_map.empty; f = Char_map.empty; pred = Char_map.empty; color = List.fold_right (fun x -> Char_map.add x White) v Char_map.empty; acc} in (snd (dfs_visit 0 c initial_state)).acc end;; module M : GRAPH
什么意思,还搞了个状态 state,其实就是我的 visited 那个 Set,还搞了个什么颜色和发现时间,题里也没要求啊。
88. Connected Components
Write a predicate that splits a graph into its connected components.
切割子图吗,那就是遍历再 remove 一下再递归呗。
我还是用原来的按个图的定义吧,上一题邻接表这个有点憨憨,还得用 Map 的东西,有点麻烦。
偷一手深度遍历。
let depth_traversal g v =
let rec neighbours v acc = function
| [] -> acc
| (x,y)::tl ->
if x = v then neighbours v (y::acc) tl
else if y = v then neighbours v (x::acc) tl
else neighbours v acc tl
in
let rec travel s (m,p) =
if List.mem s m then m,p
else List.fold_left (fun (m,p) x -> travel x (m,p)) (s::m, s::p) (neighbours s [] g.edges)
in
travel v ([],[]) |> snd;;
val depth_traversal : 'a graph_term -> 'a -> 'a list = <fun>
let split g =
let except l1 l2 = List.filter (fun e -> not (List.mem e l2)) l1 in
let rec aux nodes = match nodes with
| [] -> []
| h::t -> let visited = depth_traversal g h in
let remain = except t visited in
visited :: (aux remain)
in
aux g.nodes;;
val split : 'a graph_term -> 'a list list = <fun>
89. Bipartite Graphs
Write a predicate that finds out whether a given graph is bipartite.
遍历边,边的两个节点必须在不同侧,回溯。
讲道理这函数叫 split 是不是合适一点哦,已经被上一题占用了。
癌,其实可以多点判断剪枝的,不剪了,搞就完事了。
let is_bipartite g =
let rec aux l1 l2 remain_edges = match remain_edges with
| [] -> true
| (n1, n2)::t ->
let n1l1 = List.mem n1 l1 in
let n1l2 = List.mem n1 l2 in
let n2l1 = List.mem n2 l1 in
let n2l2 = List.mem n2 l2 in
if (n1l1 && n2l1) || (n1l2 && n2l2) then false
else if n1l1||n2l2 then aux (n1::l1) (n2::l2) t
else if n1l2||n2l1 then aux (n2::l1) (n1::l2) t
else aux (n1::l1) (n2::l2) t || aux (n2::l1) (n1::l2) t
in
aux [] [] g.edges
90. Generate K-Regular Simple Graphs With N Nodes
In a K-regular graph all nodes have a degree of K; i.e. the number of edges incident in each node is K. How many (non-isomorphic!) 3-regular graphs with 6 nodes are there?
See also the table of results.
什么情况,才发现我的题号都对不上了,也没漏题吧。
非同构的,有6个节点的 3-regular 图。生成后回溯去重。问题是怎么去重呢?我感觉会超时,这个太大了,而且特意要 6 个节点,就是要排除那些效率太低的方法,头疼啊。
let generate node_num regular =
let rec count_edges n l = match l with
| [] -> 0
| (s,e)::t -> if s=n||e=n then 1 + (count_edges n t) else count_edges n t
in
let rec aux now next edges =
let now_degree = count_edges now edges in
if now_degree = regular then aux (now+1) (now+2) edges else
if now>node_num && (List.length edges = (regular * node_num))
then [edges]
else if next>node_num then []
else if count_edges next edges <= regular then (aux now (next+1) ((now, next) :: edges)) @ aux now (next+1) (edges)
else aux now (next+1) (edges)
in
aux 1 2 [];;
val generate : int -> int -> (int * int) list list = <fun>
ops, I forget to remove the duplicate using the isomorphism.
总结
太猪了,图同构那道题写了我两天写不出来。
文档信息
- 本文作者:nyaaar
- 本文链接:https://nyaaarlathotep.github.io/2024/09/13/Ocaml-99-%E9%97%AE%E9%A2%98%E7%AC%94%E8%AE%B0-6/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)