笔记

70A. Tree Construction From a Node String

A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.

To represent multiway trees, we will use the following type which is a direct translation of the definition:

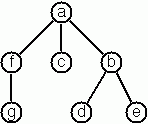
# type 'a mult_tree = T of 'a * 'a mult_tree list;;
type 'a mult_tree = T of 'a * 'a mult_tree list

The example tree depicted opposite is therefore represented by the following OCaml expression:

# T ('a', [T ('f', [T ('g', [])]); T ('c', []); T ('b', [T ('d', []); T ('e', [])])]);;
- : char mult_tree =
T ('a',
 [T ('f', [T ('g', [])]); T ('c', []); T ('b', [T ('d', []); T ('e', [])])])

We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level.

By this rule, the tree in the figure opposite is represented as: afg^^c^bd^e^^^.

Write functions string_of_tree : char mult_tree -> string to construct the string representing the tree and tree_of_string : string -> char mult_tree to construct the tree when the string is given.

# let t = T ('a', [T ('f', [T ('g', [])]); T ('c', []);
          T ('b', [T ('d', []); T ('e', [])])]);;
val t : char mult_tree =
  T ('a',
   [T ('f', [T ('g', [])]); T ('c', []); T ('b', [T ('d', []); T ('e', [])])])

来了来了。巧妙的是它是用一个多余 ^ 来表明自己的结束的，就像是自己的根上层还有父一样，正好符合递归了。

let rec string_of_tree root = 
	let rec string_of_l l = match l with
		| [] -> ""
		| h::t -> string_of_tree h ^ (string_of_l t)
	in
	match root with
		| T (v, sons) -> String.make 1 v ^ string_of_l sons ^ "^";;

val string_of_tree : char mult_tree -> string = <fun>

这个递归有点麻烦哦。呃呃呃，好像没法搞了，我这两个内部函数互相调用，但 OCaml 又不是那种申明式的，编译都无法通过吧？

完了啊，噶了，这个递归这么麻烦，我写了这么久。这下寄了。

癌，有了有了，查了下文档发现可以用 and 这样写。以前的标准答案也用过啊，傻了。

let rec tree_of_string s =
	let eat_one str = Str.string_after str 1 in
	let rec aux remain = let (sonss, remain1) = sons (eat_one remain) in
		(T(remain.[0], sonss), remain1)
	and
	sons remain = if remain.[0]='^' then ([], eat_one remain) else
		let (bro, remain1)=aux remain in
		let (other_bros, remain2) = sons remain1 in
		(bro::other_bros, remain2)
	in
	aux s;;

val tree_of_string : string -> char mult_tree * string = <fun>

咋回事呢，你把你 tree_of_string 给我交了。

又用个 buffer 是吧。

# (* We could build the final string by string concatenation but
     this is expensive due to the number of operations.  We use a
     buffer instead. *)
  let rec add_string_of_tree buf (T (c, sub)) =
    Buffer.add_char buf c;
    List.iter (add_string_of_tree buf) sub;
    Buffer.add_char buf '^'
  let string_of_tree t =
    let buf = Buffer.create 128 in
    add_string_of_tree buf t;
    Buffer.contents buf;;
val add_string_of_tree : Buffer.t -> char mult_tree -> unit = <fun>
val string_of_tree : char mult_tree -> string = <fun>

70B. Count the Nodes of a Multiway Tree

# count_nodes (T ('a', [T ('f', []) ]));;
- : int = 2

泪目了，简单的来了，和回家了一样安心。

我发现多叉树的总是要有这种复合互相调用的递归，神秘哦。

let rec count_nodes (T(v, sons)) = 
	let rec aux l = match l with
		| [] -> 0
		| h::t -> count_nodes h + aux t
	in
	1 + aux sons;;

val count_nodes : 'a mult_tree -> int = <fun>

还得是你啊，fold_left，学，好吧，学。

# let rec count_nodes (T (_, sub)) =
    List.fold_left (fun n t -> n + count_nodes t) 1 sub;;
val count_nodes : 'a mult_tree -> int = <fun>

71. Determine the Internal Path Length of a Tree

We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree. By this definition, the tree t in the figure of the previous problem has an internal path length of 9. Write a function ipl tree that returns the internal path length of tree.

# ipl t;;
- : int = 9

let ipl root = 
	let rec aux (T(v,sons)) depth = match sons with
		| [] -> depth
		| l -> List.fold_left (fun n t -> n + aux t (depth+1)) depth sons
	in
	aux root 0;;

val ipl : 'a mult_tree -> int = <fun>

哦，不用 match 的，fold_left 自然能处理 [] 的情况。

# let rec ipl_sub len (T(_, sub)) =
    (* [len] is the distance of the current node to the root.  Add the
       distance of all sub-nodes. *)
    List.fold_left (fun sum t -> sum + ipl_sub (len + 1) t) len sub
  let ipl t = ipl_sub 0 t;;
val ipl_sub : int -> 'a mult_tree -> int = <fun>
val ipl : 'a mult_tree -> int = <fun>

72. Construct the Bottom-Up Order Sequence of the Tree Nodes

Write a function bottom_up t which constructs the bottom-up sequence of the nodes of the multiway tree t.

# bottom_up (T ('a', [T ('b', [])]));;
- : char list = ['b'; 'a']
# bottom_up t;;
- : char list = ['g'; 'f'; 'c'; 'd'; 'e'; 'b'; 'a']

效率很差，用了太多次 list 连接。应该能改的好点的，传 acc 下去，List.rev 什么的。

let rec bottom_up (T(v,sons)) = 
	let son_str = List.fold_left (fun n t -> n @ bottom_up t) [] sons in
	son_str @ [v];;

val bottom_up : 'a mult_tree -> 'a list = <fun>

嗯？fold_right 吗。。。还是你牛。

# let rec prepend_bottom_up (T (c, sub)) l =
    List.fold_right (fun t l -> prepend_bottom_up t l) sub (c :: l)
  let bottom_up t = prepend_bottom_up t [];;
val prepend_bottom_up : 'a mult_tree -> 'a list -> 'a list = <fun>
val bottom_up : 'a mult_tree -> 'a list = <fun>

73. Lisp-Like Tree Representation

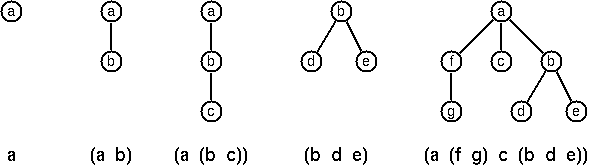
There is a particular notation for multiway trees in Lisp. The picture shows how multiway tree structures are represented in Lisp.

Note that in the “lispy” notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The “lispy” representation of a multiway tree is a sequence of atoms and parentheses ‘(‘ and ‘)’. This is very close to the way trees are represented in OCaml, except that no constructor T is used. Write a function lispy : char mult_tree -> string that returns the lispy notation of the tree.

# lispy (T ('a', []));;
- : string = "a"
# lispy (T ('a', [T ('b', [])]));;
- : string = "(a b)"
# lispy t;;
- : string = "(a (f g) c (b d e))"

lisp 是这么表达树的吗，很神秘哦。

let rec lispy (T(v,sons)) = match sons with
	| [] -> String.make 1 v
	| l -> "(" ^ (String.make 1 v) ^ (List.fold_left (fun n t-> n ^ " " ^ lispy t) "" l) ^ ")";;

val lispy : char mult_tree -> string = <fun>

又玩你的 buffer 是吧。哦，可以 iter，因为没有 fold 的初始值，差不多吧。

# let rec add_lispy buf = function
    | T(c, []) -> Buffer.add_char buf c
    | T(c, sub) ->
       Buffer.add_char buf '(';
       Buffer.add_char buf c;
       List.iter (fun t -> Buffer.add_char buf ' '; add_lispy buf t) sub;
       Buffer.add_char buf ')'
  let lispy t =
    let buf = Buffer.create 128 in
    add_lispy buf t;
    Buffer.contents buf;;
val add_lispy : Buffer.t -> char mult_tree -> unit = <fun>
val lispy : char mult_tree -> string = <fun>

总结

多路树和二叉树不同比想象的大哦，是个 list 递归的时候麻烦一点。