笔记

45. Construct Completely Balanced Binary Trees

A binary tree is either empty or it is composed of a root element and two successors, which are binary trees themselves.

In OCaml, one can define a new type binary_tree that carries an arbitrary value of type 'a (thus is polymorphic) at each node.

# type 'a binary_tree =
  | Empty
  | Node of 'a * 'a binary_tree * 'a binary_tree;;
type 'a binary_tree = Empty | Node of 'a * 'a binary_tree * 'a binary_tree

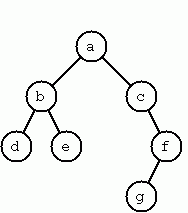
An example of tree carrying char data is:

# let example_tree =
  Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
       Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)));;
val example_tree : char binary_tree =
  Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
   Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)))

In OCaml, the strict type discipline guarantees that, if you get a value of type binary_tree, then it must have been created with the two constructors Empty and Node.

In a completely balanced binary tree, the following property holds for every node: The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal, which means their difference is not greater than one.

Write a function cbal_tree to construct completely balanced binary trees for a given number of nodes. The function should generate all solutions via backtracking. Put the letter 'x' as information into all nodes of the tree.

# cbal_tree 4;;
- : char binary_tree/2 list =
[Node ('x', Node ('x', Empty, Empty),
  Node ('x', Node ('x', Empty, Empty), Empty));
 Node ('x', Node ('x', Empty, Empty),
  Node ('x', Empty, Node ('x', Empty, Empty)));
 Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
  Node ('x', Empty, Empty));
 Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
  Node ('x', Empty, Empty))]

奇妙啊，这图还是 gif 格式的，意思是比 jpg 更小？

backtracking 在哪了，交换左右数量吗？那也行。

let rec cbal_tree num = match num with
	| 0 -> [Empty]
	| 1 -> [Node ('x', Empty, Empty)]
	| n -> 
		let left = (n-1)/2 in let right = n-1-left in 
		if left = right then 
			let nodes = cbal_tree left in
			List.flatten (List.map (fun l -> List.map (fun r -> Node('x', l, r)) nodes) nodes)
		else
			let left_num_nodes = cbal_tree left in
			let right_num_nodes = cbal_tree right in
			List.flatten (List.map (fun l -> List.map (fun r -> Node('x', l, r)) right_num_nodes) left_num_nodes) @ List.flatten (List.map (fun l -> List.map (fun r -> Node('x', l, r)) left_num_nodes) right_num_nodes);;

val cbal_tree : int -> char binary_tree list = <fun>

看起来 fold_left 就是个针对 acc 特化的函数，这样就不存在我这种 list 嵌套还得打平多余的一步了。

# (* Build all trees with given [left] and [right] subtrees. *)
  let add_trees_with left right all =
    let add_right_tree all l =
      List.fold_left (fun a r -> Node ('x', l, r) :: a) all right in
    List.fold_left add_right_tree all left

  let rec cbal_tree n =
    if n = 0 then [Empty]
    else if n mod 2 = 1 then
      let t = cbal_tree (n / 2) in
      add_trees_with t t []
    else (* n even: n-1 nodes for the left & right subtrees altogether. *)
      let t1 = cbal_tree (n / 2 - 1) in
      let t2 = cbal_tree (n / 2) in
      add_trees_with t1 t2 (add_trees_with t2 t1 []);;
val add_trees_with :
  char binary_tree list ->
  char binary_tree list -> char binary_tree list -> char binary_tree list =
  <fun>
val cbal_tree : int -> char binary_tree list = <fun>

46. Symmetric Binary Trees

Let us call a binary tree symmetric if you can draw a vertical line through the root node and then the right subtree is the mirror image of the left subtree. Write a function is_symmetric to check whether a given binary tree is symmetric.

Hint: Write a function is_mirror first to check whether one tree is the mirror image of another. We are only interested in the structure, not in the contents of the nodes.

来了来了，感觉像在做 LeetCode。这个提示有啥用呢，不是同时就对比了，还用搞这么麻烦吗。不对，撒情况，没有测试用例吗。

let rec is_symmetric t1 t2 = match t1 with
	| Empty -> let res = match t2 with 
		| Empty -> true
		| _ -> false
		in
		res
	| Node(t1v,t1l,t1r) -> match t2 with 
		| Empty -> false
		| Node(t2v,t2l,t2r) -> t1v=t2v && is_symmetric t1l t2r && is_symmetric t1r t2l;;

val is_symmetric : 'a binary_tree -> 'a binary_tree -> bool = <fun>

哦，弱智了，原来这个意思。。。我改下

let rec is_symmetric t = 
	let rec is_mirror t1 t2 =
    match t1, t2 with
    | Empty, Empty -> true
    | Node(_, l1, r1), Node(_, l2, r2) ->
       is_mirror l1 r2 && is_mirror r1 l2
    | _ -> false
    in
	match t with
		| Empty -> true
		| Node(_, l, r) -> is_mirror l r;;

val is_symmetric : 'a binary_tree -> bool = <fun>

还是你牛，还能这么 match 的。。。

# let rec is_mirror t1 t2 =
    match t1, t2 with
    | Empty, Empty -> true
    | Node(_, l1, r1), Node(_, l2, r2) ->
       is_mirror l1 r2 && is_mirror r1 l2
    | _ -> false

  let is_symmetric = function
    | Empty -> true
    | Node(_, l, r) -> is_mirror l r;;
val is_mirror : 'a binary_tree -> 'b binary_tree -> bool = <fun>
val is_symmetric : 'a binary_tree -> bool = <fun>

47. Binary Search Trees (Dictionaries)

Construct a binary search tree from a list of integer numbers.

# construct [3; 2; 5; 7; 1];;
- : int binary_tree =
Node (3, Node (2, Node (1, Empty, Empty), Empty),
 Node (5, Empty, Node (7, Empty, Empty)))

Then use this function to test the solution of the previous problem.

# is_symmetric (construct [5; 3; 18; 1; 4; 12; 21]);;
- : bool = true
# not (is_symmetric (construct [3; 2; 5; 7; 4]));;
- : bool = true

奥，这道题测上道题。

let construct nums = 
	let rec add root next = match root with
		| Empty -> Node(next, Empty, Empty)
		| Node(v,l,r) -> if next>v then Node(v,l,(add r next)) else Node(v,(add l next),r)
	in
	let rec build remain root = match remain with
		| [] -> root
		| h::t -> build t (add root h) 
	in
	match nums with
		| [] -> Empty
		| h::t -> build t (Node(h, Empty, Empty))

哦，牛逼，好像是这么个意思，就是 fold_left 啊，简化了好多。

# let rec insert tree x = match tree with
    | Empty -> Node (x, Empty, Empty)
    | Node (y, l, r) ->
       if x = y then tree
       else if x < y then Node (y, insert l x, r)
       else Node (y, l, insert r x)
  let construct l = List.fold_left insert Empty l;;
val insert : 'a binary_tree -> 'a -> 'a binary_tree = <fun>
val construct : 'a list -> 'a binary_tree = <fun>

48. Generate-and-Test Paradigm

Apply the generate-and-test paradigm to construct all symmetric, completely balanced binary trees with a given number of nodes.

# sym_cbal_trees 5;;
- : char binary_tree list =
[Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
  Node ('x', Empty, Node ('x', Empty, Empty)));
 Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
  Node ('x', Node ('x', Empty, Empty), Empty))]

How many such trees are there with 57 nodes? Investigate about how many solutions there are for a given number of nodes? What if the number is even? Write an appropriate function.

# List.length (sym_cbal_trees 57);;
- : int = 256

组合一下的意思？

let sym_cbal_trees n = 
	let all = cbal_tree n in
	List.filter (fun t -> is_symmetric t) all;;

val sym_cbal_trees : int -> char binary_tree list = <fun>

# let sym_cbal_trees n =
    List.filter is_symmetric (cbal_tree n);;
val sym_cbal_trees : int -> char binary_tree list = <fun>

49. Construct Height-Balanced Binary Trees

In a height-balanced binary tree, the following property holds for every node: The height of its left subtree and the height of its right subtree are almost equal, which means their difference is not greater than one.

Write a function hbal_tree to construct height-balanced binary trees for a given height. The function should generate all solutions via backtracking. Put the letter 'x' as information into all nodes of the tree.

# let t = hbal_tree 3;;
val t : char binary_tree list =
  [Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
    Node ('x', Empty, Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
    Node ('x', Node ('x', Empty, Empty), Empty));
   Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
    Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
    Node ('x', Empty, Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
    Node ('x', Node ('x', Empty, Empty), Empty));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
    Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
    Node ('x', Empty, Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
    Node ('x', Node ('x', Empty, Empty), Empty));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
    Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
    Node ('x', Empty, Empty));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
    Node ('x', Empty, Empty));
   Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
    Node ('x', Empty, Empty));
   Node ('x', Node ('x', Empty, Empty),
    Node ('x', Empty, Node ('x', Empty, Empty)));
   Node ('x', Node ('x', Empty, Empty),
    Node ('x', Node ('x', Empty, Empty), Empty));
   Node ('x', Node ('x', Empty, Empty),
    Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)))]

换高度了。让我试试 fold_left。

let add_trees_with left right all = 
	let add_right_tree all l =
    	List.fold_left (fun a r -> Node ('x', l, r) :: a) all right in
    List.fold_left add_right_tree all left
let rec hbal_tree h = match h with
	| 1 -> [Node('x', Empty, Empty)]
	| 2 -> [Node('x', Node('x', Empty, Empty), Empty);Node('x', Empty, Node('x', Empty, Empty));Node('x', Node('x', Empty, Empty), Node('x', Empty, Empty))]
	| n -> add_trees_with (hbal_tree (n-1)) (hbal_tree (n-1)) (add_trees_with (hbal_tree (n-1)) (hbal_tree (n-2)) (add_trees_with (hbal_tree (n-2)) (hbal_tree (n-1)) []))

不是，这咋验证啊，太多了盯不过来。

# let rec hbal_tree n =
    if n = 0 then [Empty]
    else if n = 1 then [Node ('x', Empty, Empty)]
    else
    (* [add_trees_with left right trees] is defined in a question above. *)
      let t1 = hbal_tree (n - 1)
      and t2 = hbal_tree (n - 2) in
      add_trees_with t1 t1 (add_trees_with t1 t2 (add_trees_with t2 t1 []));;
val hbal_tree : int -> char binary_tree list = <fun>

50. Construct Height-Balanced Binary Trees With a Given Number of Nodes

Consider a height-balanced binary tree of height h. What is the maximum number of nodes it can contain? Clearly, max_nodes = 2h - 1.

# let max_nodes h = 1 lsl h - 1;;
val max_nodes : int -> int = <fun>

Minimum of nodes

However, what is the minimum number min_nodes? This question is more difficult. Try to find a recursive statement and turn it into a function min_nodes defined as follows: min_nodes h returns the minimum number of nodes in a height-balanced binary tree of height h.

Minimum height

On the other hand, we might ask: what are the minimum (resp. maximum) height H a height-balanced binary tree with N nodes can have? min_height (resp. max_height n) returns the minimum (resp. maximum) height of a height-balanced binary tree with n nodes.

Constructing trees

Now, we can attack the main problem: construct all the height-balanced binary trees with a given number of nodes. hbal_tree_nodes n returns a list of all height-balanced binary tree with n nodes.

Find out how many height-balanced trees exist for n = 15.

	# List.length (hbal_tree_nodes 15);;
- : int = 1553

你这一道顶三道啊，头疼。癌，好像都是必要的前置步骤了，我服了。

let rec min_nodes n = if n = 0 then 0 
	else if n=1 then 1
	else (min_nodes (n-1))+1+(min_nodes (n-2))

let int_pow a b= int_of_float ((float_of_int a) ** (float_of_int b));;

val int_pow : int -> int -> int = <fun>

let min_height n = 	
	let rec aux count = if (int_pow 2 count)-1>=n then count else aux (count+1) in
	aux 0

let max_height n = 
	let rec aux now = if min_nodes now<=n then aux (now+1) else now-1
	in
	aux 0

受不了了，这个回溯太麻烦了，直接抄。完了，答案也看不懂了。

看了半天了，呃呃呃，和我想得差不多，先找到 nodes 对应的可能的所有高度，然后对应子树的高度可能为（h-1，h-1），（h-1，h-2），还有互换左右支的情况。同时，再把总的 nodes 分配到左右支，这又是一个遍历，并同时保证左右支的平衡（这里直接递归了）。

巧妙的是这个 fold_range 的运用，这两次遍历都用这个了，acc 到最后的结果，很方便。但这个 ~ 是什么意思啊，而且定义里的参数的位置和标准答案里的参数的位置不一样，什么意思。

# let rec fold_range ~f ~init n0 n1 =
    if n0 > n1 then init else fold_range ~f ~init:(f init n0) (n0 + 1) n1;;
val fold_range : f:('a -> int -> 'a) -> init:'a -> int -> int -> 'a = <fun>

还有那个经典的两遍 fold_left，让两个列表作为左右子树结合出了所有可能的结果。

        List.fold_left (fun l t1 ->
            List.fold_left (fun l t2 -> Node ('x', t1, t2) :: l) l t2) l t1
      )

交换左右子树，并积累结果。

# let rec add_swap_left_right trees =
    List.fold_left (fun a n -> match n with
                               | Node (v, t1, t2) -> Node (v, t2, t1) :: a
                               | Empty -> a) trees trees;;
val add_swap_left_right : 'a binary_tree list -> 'a binary_tree list = <fun>

标准答案：

# let rec hbal_tree_nodes_height h n =
    assert(min_nodes h <= n && n <= max_nodes h);
    if h = 0 then [Empty]
    else
      let acc = add_hbal_tree_node [] (h - 1) (h - 2) n in
      let acc = add_swap_left_right acc in
      add_hbal_tree_node acc (h - 1) (h - 1) n
  and add_hbal_tree_node l h1 h2 n =
    let min_n1 = max (min_nodes h1) (n - 1 - max_nodes h2) in
    let max_n1 = min (max_nodes h1) (n - 1 - min_nodes h2) in
    fold_range min_n1 max_n1 ~init:l ~f:(fun l n1 ->
        let t1 = hbal_tree_nodes_height h1 n1 in
        let t2 = hbal_tree_nodes_height h2 (n - 1 - n1) in
        List.fold_left (fun l t1 ->
            List.fold_left (fun l t2 -> Node ('x', t1, t2) :: l) l t2) l t1
      )
      let hbal_tree_nodes n =
    fold_range (min_height n) (max_height n) ~init:[] ~f:(fun l h ->
        List.rev_append (hbal_tree_nodes_height h n) l);;
val hbal_tree_nodes_height : int -> int -> char binary_tree list = <fun>
val add_hbal_tree_node :
  char binary_tree list -> int -> int -> int -> char binary_tree list = <fun>
val hbal_tree_nodes : int -> char binary_tree list = <fun>

51. Count the Leaves of a Binary Tree

A leaf is a node with no successors. Write a function count_leaves to count them.

# count_leaves Empty;;
- : int = 0

雷姆了，终于正常多了。

let rec count_leaves root = match root with
	| Empty -> 0
	| Node(v, Empty, Empty) -> 1
	| Node(b, l, r) -> count_leaves l + count_leaves r;;

val count_leaves : 'a binary_tree -> int = <fun>

# let rec count_leaves = function
    | Empty -> 0
    | Node (_, Empty, Empty) -> 1
    | Node (_, l, r) -> count_leaves l + count_leaves r;;
val count_leaves : 'a binary_tree -> int = <fun>

52. Collect the Leaves of a Binary Tree in a List

A leaf is a node with no successors. Write a function leaves to collect them in a list.

# leaves Empty;;
- : 'a list = []

let rec leaves root =  match root with
	| Empty -> []
	| Node(v, Empty, Empty) -> [v]
	| Node(b, l, r) -> leaves l @ leaves r;;

val leaves : 'a binary_tree -> 'a list = <fun>

癌，被标准答案预判了。

# (* Having an accumulator acc prevents using inefficient List.append.
   * Every Leaf will be pushed directly into accumulator.
   * Not tail-recursive, but that is no problem since we have a binary tree and
   * and stack depth is logarithmic. *)
  let leaves t = 
    let rec leaves_aux t acc = match t with
      | Empty -> acc
      | Node (x, Empty, Empty) -> x :: acc
      | Node (x, l, r) -> leaves_aux l (leaves_aux r acc)
    in
    leaves_aux t [];;
val leaves : 'a binary_tree -> 'a list = <fun>

53. Collect the Internal Nodes of a Binary Tree in a List

An internal node of a binary tree has either one or two non-empty successors. Write a function internals to collect them in a list.

# internals (Node ('a', Empty, Empty));;
- : char list = []

let internals t = 
	let rec aux root acc = match root with
		| Empty -> acc
        | Node (x, Empty, Empty) -> acc
        | Node (x, l, r) -> aux l (aux r (Node(x, l, r)::acc))
    in
    aux t [];;

val internals : 'a binary_tree -> 'b list = <fun>

哦，最好保持顺序，中序，我这个是什么鬼顺序，根 右 左。

# (* Having an accumulator acc prevents using inefficient List.append.
   * Every internal node will be pushed directly into accumulator.
   * Not tail-recursive, but that is no problem since we have a binary tree and
   * and stack depth is logarithmic. *)
  let internals t = 
    let rec internals_aux t acc = match t with
      | Empty -> acc
      | Node (x, Empty, Empty) -> acc
      | Node (x, l, r) -> internals_aux l (x :: internals_aux r acc)
    in
    internals_aux t [];;
val internals : 'a binary_tree -> 'a list = <fun>

54. Collect the Nodes at a Given Level in a List

A node of a binary tree is at level N if the path from the root to the node has length N-1. The root node is at level 1. Write a function at_level t l to collect all nodes of the tree t at level l in a list.

# let example_tree =
  Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
       Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)));;
val example_tree : char binary_tree =
  Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
   Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)))
# at_level example_tree 2;;
- : char list = ['b'; 'c']

Using at_level it is easy to construct a function levelorder which creates the level-order sequence of the nodes. However, there are more efficient ways to do that.

let at_level root height = 
	let rec aux r h acc = match r with
		| Empty -> acc
		| Node(v, l, r) -> if h=1 then v::acc 
			else aux l (h-1) (aux r (h-1) acc)
	in
	aux root height [];;

val at_level : 'a binary_tree -> int -> 'a list = <fun>

又和我方向反了，我这个算更正统的递归好吧。

# (* Having an accumulator acc prevents using inefficient List.append.
   * Every node at level N will be pushed directly into accumulator.
   * Not tail-recursive, but that is no problem since we have a binary tree and
   * and stack depth is logarithmic. *)
  let at_level t level =
    let rec at_level_aux t acc counter = match t with
      | Empty -> acc
      | Node (x, l, r) ->
        if counter=level then
          x :: acc
        else
          at_level_aux l (at_level_aux r acc (counter + 1)) (counter + 1)
    in
      at_level_aux t [] 1;;
val at_level : 'a binary_tree -> int -> 'a list = <fun>

55. Construct a Complete Binary Tree

A complete binary tree with height H is defined as follows: The levels 1,2,3,…,H-1 contain the maximum number of nodes (i.e 2i-1 at the level i, note that we start counting the levels from 1 at the root). In level H, which may contain less than the maximum possible number of nodes, all the nodes are “left-adjusted”. This means that in a levelorder tree traversal all internal nodes come first, the leaves come second, and empty successors (the nil’s which are not really nodes!) come last.

Particularly, complete binary trees are used as data structures (or addressing schemes) for heaps.

We can assign an address number to each node in a complete binary tree by enumerating the nodes in levelorder, starting at the root with number 1. In doing so, we realize that for every node X with address A the following property holds: The address of X’s left and right successors are 2A and 2A+1, respectively, supposed the successors do exist. This fact can be used to elegantly construct a complete binary tree structure. Write a function is_complete_binary_tree with the following specification: is_complete_binary_tree n t returns true iff t is a complete binary tree with n nodes.

# complete_binary_tree [1; 2; 3; 4; 5; 6];;
- : int binary_tree =
Node (1, Node (2, Node (4, Empty, Empty), Node (5, Empty, Empty)),
 Node (3, Node (6, Empty, Empty), Empty))

OCaml，或者说这些函数式语言，列表取址是 O(n) 的啊，还有什么好方法吗？

let complete_binary_tree list = 
	let rec get_index i l= match l with
		| []-> raise Not_found
		| h::t -> if i = 1 then h else get_index (i-1) t
	in
	let rec make_node index = if index>List.length list then Empty else
		Node(get_index index list, make_node (2*index), make_node (2*index + 1))
	in
	make_node 1

split 吗，神秘啊，没太看明白。哦，这个 lsl 是逻辑左移位。

我好像又看明白了，比起我每次都寻址，它做了个切片，少了些重复递归的过程，然后也是递归了，用 myflatten。

# let rec split_n lst acc n = match (n, lst) with
    | (0, _) -> (List.rev acc, lst)
    | (_, []) -> (List.rev acc, [])
    | (_, h :: t) -> split_n t (h :: acc) (n-1)

  let rec myflatten p c = 
    match (p, c) with
    | (p, []) -> List.map (fun x -> Node (x, Empty, Empty)) p
    | (x :: t, [y]) -> Node (x, y, Empty) :: myflatten t []
    | (ph :: pt, x :: y :: t) -> (Node (ph, x, y)) :: myflatten pt t
    | _ -> invalid_arg "myflatten"

  let complete_binary_tree = function
    | [] -> Empty
    | lst ->
       let rec aux l = function
         | [] -> []
         | lst -> let p, c = split_n lst [] (1 lsl l) in
                  myflatten p (aux (l + 1) c)
       in
         List.hd (aux 0 lst);;
val split_n : 'a list -> 'a list -> int -> 'a list * 'a list = <fun>
val myflatten : 'a list -> 'a binary_tree list -> 'a binary_tree list = <fun>
val complete_binary_tree : 'a list -> 'a binary_tree = <fun>

56. Layout a Binary Tree (1)

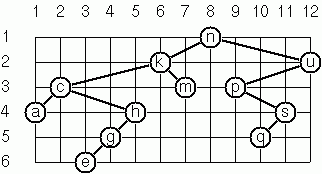
As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration.

In this layout strategy, the position of a node v is obtained by the following two rules:

• x(v) is equal to the position of the node v in the inorder sequence;
• y(v) is equal to the depth of the node v in the tree.

In order to store the position of the nodes, we will enrich the value at each node with the position (x,y).

The tree pictured above is

# let example_layout_tree =
  let leaf x = Node (x, Empty, Empty) in
  Node ('n', Node ('k', Node ('c', leaf 'a',
                           Node ('h', Node ('g', leaf 'e', Empty), Empty)),
                 leaf 'm'),
       Node ('u', Node ('p', Empty, Node ('s', leaf 'q', Empty)), Empty));;
val example_layout_tree : char binary_tree =
  Node ('n',
   Node ('k',
    Node ('c', Node ('a', Empty, Empty),
     Node ('h', Node ('g', Node ('e', Empty, Empty), Empty), Empty)),
    Node ('m', Empty, Empty)),
   Node ('u', Node ('p', Empty, Node ('s', Node ('q', Empty, Empty), Empty)),
    Empty))
# layout_binary_tree_1 example_layout_tree;;
- : (char * int * int) binary_tree =
Node (('n', 8, 1),
 Node (('k', 6, 2),
  Node (('c', 2, 3), Node (('a', 1, 4), Empty, Empty),
   Node (('h', 5, 4),
    Node (('g', 4, 5), Node (('e', 3, 6), Empty, Empty), Empty), Empty)),
  Node (('m', 7, 3), Empty, Empty)),
 Node (('u', 12, 2),
  Node (('p', 9, 3), Empty,
   Node (('s', 11, 4), Node (('q', 10, 5), Empty, Empty), Empty)),
  Empty))

好说好说。

let layout_binary_tree_1 root = 
	let rec aux left_start node depth = match node with
		| Empty -> (left_start,Empty)
		| Node(v,l,r) -> let left_num, left_tree = aux left_start l (depth+1) in
			let right_num, right_tree = aux (left_num+1) r (depth + 1) in
        	(right_num, Node((v, left_num, depth), left_tree, right_tree))
    in
	let (total_num, r) = aux 1 root 1 in
	r;;

val layout_binary_tree_1 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

这不是完全一样吗。改下，不用最后这步多余的了。

let layout_binary_tree_1 root = 
	let rec aux left_start node depth = match node with
		| Empty -> (left_start,Empty)
		| Node(v,l,r) -> let left_num, left_tree = aux left_start l (depth+1) in
			let right_num, right_tree = aux (left_num+1) r (depth + 1) in
        	(right_num, Node((v, left_num, depth), left_tree, right_tree))
    in
	snd (aux 1 root 1)

val layout_binary_tree_1 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

# let layout_binary_tree_1 t =
    let rec layout depth x_left = function
      (* This function returns a pair: the laid out tree and the first
       * free x location *)
      | Empty -> (Empty, x_left)
      | Node (v,l,r) ->
         let (l', l_x_max) = layout (depth + 1) x_left l in
         let (r', r_x_max) = layout (depth + 1) (l_x_max + 1) r in
           (Node ((v, l_x_max, depth), l', r'), r_x_max)
    in
      fst (layout 1 1 t);;
val layout_binary_tree_1 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

57. Layout a Binary Tree (2)

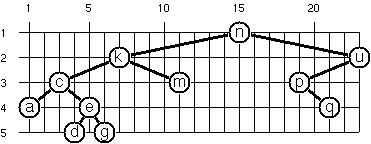
An alternative layout method is depicted in this illustration. Find out the rules and write the corresponding OCaml function.

Hint: On a given level, the horizontal distance between neighbouring nodes is constant.

The tree shown is

# let example_layout_tree =
  let leaf x = Node (x, Empty, Empty) in
  Node ('n', Node ('k', Node ('c', leaf 'a',
                           Node ('e', leaf 'd', leaf 'g')),
                 leaf 'm'),
       Node ('u', Node ('p', Empty, leaf 'q'), Empty));;
val example_layout_tree : char binary_tree =
  Node ('n',
   Node ('k',
    Node ('c', Node ('a', Empty, Empty),
     Node ('e', Node ('d', Empty, Empty), Node ('g', Empty, Empty))),
    Node ('m', Empty, Empty)),
   Node ('u', Node ('p', Empty, Node ('q', Empty, Empty)), Empty))
# layout_binary_tree_2 example_layout_tree ;;
- : (char * int * int) binary_tree =
Node (('n', 15, 1),
 Node (('k', 7, 2),
  Node (('c', 3, 3), Node (('a', 1, 4), Empty, Empty),
   Node (('e', 5, 4), Node (('d', 4, 5), Empty, Empty),
    Node (('g', 6, 5), Empty, Empty))),
  Node (('m', 11, 3), Empty, Empty)),
 Node (('u', 23, 2),
  Node (('p', 19, 3), Empty, Node (('q', 21, 4), Empty, Empty)), Empty))

初看麻烦，其实两个兄弟节点之间就是 2^n 的距离，需要先扫描一下最高层数。

有点绕，节点需要告诉自己的左子树可以到达的最左端是多少，同时需要左子树告诉自己，自己的位置，同时再根据自己的位置告诉右子树能到达的最左端是多少，最后返回父节点应该在的位置。

不太对劲，这么搞是错误的，没法对称了，没有节点的部分会被压缩，必须由父节点来决定子节点的位置，但这个位置又是个相对位置，癌，麻烦，我就是不想多走这一遍，狗屎啊。

let layout_binary_tree_2 r = 
	let rec height root = match root with
		| Empty -> 0
		| Node(v,l,r) -> max (height l) (height r)  +1
	in
	let h = height r in
	let rec aux node left_start depth = match node with
		| Empty -> (Empty, left_start)
		| Node(v, l, r) -> let (l_tree, pos) = aux l left_start (depth+1) in
			let fater_pos = pos + (int_pow 2 (h-depth)) in
			let (r_tree, right_son_pos) = aux r (pos+1) (depth+1) in
			(Node((v, pos, depth), l_tree, r_tree), fater_pos)
	in
	fst (aux r 1 1);;

val layout_binary_tree_2 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

好处是现在可读性好了很多哦。查高度的和查根节点位置的两次遍历其实可以合并。

let layout_binary_tree_2 r = 
	let rec height root = match root with
		| Empty -> 0
		| Node(v,l,r) -> max (height l) (height r)  +1
	in
	let h = height r in
	let rec get_left_most root acc depth = match root with
		| Empty -> acc
		| Node(v,l,r) -> get_left_most l (acc + int_pow 2 (h-depth-1)) (depth + 1)
	in
	let root_pos = get_left_most r 0 1 in
	let rec rectify_tree root pos depth= match root with
		| Empty -> Empty
		| Node(v, l, r) -> let next_dis=(int_pow 2 (h-depth-1)) in
			Node((v,pos,depth), rectify_tree l (pos-next_dis) (depth+1), rectify_tree r (pos + next_dis) (depth+1))
	in
	rectify_tree r root_pos 1;;

val layout_binary_tree_2 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

因为没有 int 的 pow，所以就用左移位，你说你这不是自己给自己找罪受吗？

find_missing_left和translate_dst实际上就是找根节点的坐标，还搞得更不直观了，感觉不如我好吧。

# let layout_binary_tree_2 t =
    let rec height = function
      | Empty -> 0
      | Node (_, l, r) -> 1 + max (height l) (height r) in
    let tree_height = height t in
    let rec find_missing_left depth = function
      | Empty -> tree_height - depth
      | Node (_, l, _) -> find_missing_left (depth + 1) l in
    let translate_dst = 1 lsl (find_missing_left 0 t) - 1 in
                        (* remember than 1 lsl a = 2ᵃ *)
    let rec layout depth x_root = function
      | Empty -> Empty
      | Node (x, l, r) ->
         let spacing = 1 lsl (tree_height - depth - 1) in
         let l' = layout (depth + 1) (x_root - spacing) l
         and r' = layout (depth + 1) (x_root + spacing) r in
           Node((x, x_root, depth), l',r') in
    layout 1 ((1 lsl (tree_height - 1)) - translate_dst) t;;
val layout_binary_tree_2 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

58. Layout a Binary Tree (3)

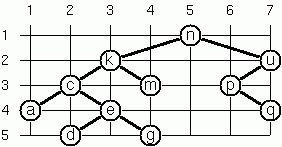
Yet another layout strategy is shown in the above illustration. The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding predicate.

Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree? This is a difficult problem. Don’t give up too early!

# let example_layout_tree =
  let leaf x = Node (x, Empty, Empty) in
  Node ('n', Node ('k', Node ('c', leaf 'a',
                           Node ('h', Node ('g', leaf 'e', Empty), Empty)),
                 leaf 'm'),
       Node ('u', Node ('p', Empty, Node ('s', leaf 'q', Empty)), Empty));;
val example_layout_tree : char binary_tree =
  Node ('n',
   Node ('k',
    Node ('c', Node ('a', Empty, Empty),
     Node ('h', Node ('g', Node ('e', Empty, Empty), Empty), Empty)),
    Node ('m', Empty, Empty)),
   Node ('u', Node ('p', Empty, Node ('s', Node ('q', Empty, Empty), Empty)),
    Empty))
# layout_binary_tree_3 example_layout_tree ;;
- : (char * int * int) binary_tree =
Node (('n', 5, 1),
 Node (('k', 3, 2),
  Node (('c', 2, 3), Node (('a', 1, 4), Empty, Empty),
   Node (('h', 3, 4),
    Node (('g', 2, 5), Node (('e', 1, 6), Empty, Empty), Empty), Empty)),
  Node (('m', 4, 3), Empty, Empty)),
 Node (('u', 7, 2),
  Node (('p', 6, 3), Empty,
   Node (('s', 7, 4), Node (('q', 6, 5), Empty, Empty), Empty)),
  Empty))

Which layout do you like most?

这道题我想了好久了，实在是难啊，没有头绪。不好递归，子树会影响父，兄弟间又会互相影响。题里的maintaining a certain symmetry in every node又是怎么个对称法，我实在是说不出话。提示说Consider the horizontal distance between a node and its successor nodes我也没看出啥来，哭了。

试着写写吧。

let layout_binary_tree_3 r = 
	let rec detect left right acc = match left, right with
		| [],_ -> acc
		| _, [] -> acc
		| (h1l,h1r)::t1, (h2l,h2r)::t2 -> if h1r+h2l > 2*acc 
			then let new_acc = ((h1r+h2l)/2)*2 in detect t1 t2 new_acc
			else detect t1 t2 acc
	in
	let rec merge left right acc = match left, right with
		| [],[] -> []
		| [],(h2l,h2r)::t -> (h2l-acc, h2r-acc)::(merge [] t acc)
		| (h1l, h1r)::t,[] -> (h1l+acc, h1r+acc)::(merge t [] acc)
		| (h1l,h1r)::t1, (h2l,h2r)::t2 -> (h1l-acc,h2r+acc)::(merge t1 t2 acc)
	in
		
	let rec aux root = match root with
		| Empty -> (0,0)
		| Node(v,l,r) -> let l_width=aux l in let r_width=aux r in
        	let width = detect l_width r_width 1 in
        	(width, width)
        	
	in
	let l

做不出来，我服了。感觉就差几步了，我也有这个 merge 以及 dist 察看子树之间最大的距离。还是有点没看懂，头疼。

In order to pack the tree tightly, the layout function will return in addition to the layout of the tree the left and right profiles of the tree, that is lists of offsets relative to the position of the root node of the tree.

# let layout_binary_tree_3 =
    let rec translate_x d = function
      | Empty -> Empty
      | Node ((v, x, y), l, r) ->
         Node ((v, x + d, y), translate_x d l, translate_x d r) in
    (* Distance between a left subtree given by its right profile [lr]
       and a right subtree given by its left profile [rl]. *)
    let rec dist lr rl = match lr, rl with
      | lrx :: ltl, rlx :: rtl -> max (lrx - rlx) (dist ltl rtl)
      | [], _ | _, [] -> 0 in
    let rec merge_profiles p1 p2 = match p1, p2 with
      | x1 :: tl1, _ :: tl2 -> x1 :: merge_profiles tl1 tl2
      | [], _ -> p2
      | _, [] -> p1 in
    let rec layout depth = function
      | Empty -> ([], Empty, [])
      | Node (v, l, r) ->
         let (ll, l', lr) = layout (depth + 1) l in
         let (rl, r', rr) = layout (depth + 1) r in
         let d = 1 + dist lr rl / 2 in
         let ll = List.map (fun x -> x - d) ll
         and lr = List.map (fun x -> x - d) lr
         and rl = List.map ((+) d) rl
         and rr = List.map ((+) d) rr in
         (0 :: merge_profiles ll rl,
          Node((v, 0, depth), translate_x (-d) l', translate_x d r'),
          0 :: merge_profiles rr lr) in
    fun t -> let (l, t', _) = layout 1 t in
             let x_min = List.fold_left min 0 l in
             translate_x (1 - x_min) t';;
val layout_binary_tree_3 : 'a binary_tree -> ('a * int * int) binary_tree =
  <fun>

59. A String Representation of Binary Trees

Somebody represents binary trees as strings of the following type (see example): "a(b(d,e),c(,f(g,)))".

• Write an OCaml function string_of_tree which generates this string representation, if the tree is given as usual (as Empty or Node(x,l,r) term). Then write a function tree_of_string which does this inverse; i.e. given the string representation, construct the tree in the usual form. Finally, combine the two predicates in a single function tree_string which can be used in both directions.
• Write the same predicate tree_string using difference lists and a single predicate tree_dlist which does the conversion between a tree and a difference list in both directions.

For simplicity, suppose the information in the nodes is a single letter and there are no spaces in the string.

# let example_layout_tree =
  let leaf x = Node (x, Empty, Empty) in
    (Node ('a', Node ('b', leaf 'd', leaf 'e'),
     Node ('c', Empty, Node ('f', leaf 'g', Empty))));;
val example_layout_tree : char binary_tree =
  Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
   Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)))

坏了，又看不懂题了，呜呜呜。difference lists指什么？

查了半天，string 还是得按地址取。还是现代的数组切片好用啊，这个 string 处理真的搞得我头疼，OCaml 本身没有的东西导致正则也不好用。

let rec string_of_tree r = match r with
	| Empty -> ""
	| Node(v,Empty,Empty) -> v
	| Node(v,l,r) -> v ^ "(" ^ string_of_tree l ^ "," ^ string_of_tree r ^ ")";;

let rec tree_of_string s = 
	if String.length s = 1 then Node(s,Empty,Empty)
	else if String.length s = 0 then Empty
	else
	let v = s.[0] in
	let s = Str.string_after (Str.string_before s ((String.length s) -1)) 2 in
	let rec div n bracket = if s.[n]=',' && bracket = 0 then 
		(Str.string_before s n,Str.string_after s (n+1))
		else if s.[n]='(' then div (n+1) (bracket+1)
		else if s.[n]=')' then div (n+1) (bracket-1)
		else div (n+1) bracket
	in
	let (l_tree,r_tree) = div 0 0 in
	Node(String.make 1 v,tree_of_string l_tree,tree_of_string r_tree)
	

还搞了个 buffer，看来字符串拼接在哪都很消耗资源。

A simple solution is:

# let rec string_of_tree = function
    | Empty -> ""
    | Node(data, l, r) ->
       let data = String.make 1 data in
       match l, r with
       | Empty, Empty -> data
       | _, _ -> data ^ "(" ^ (string_of_tree l)
                 ^ "," ^ (string_of_tree r) ^ ")";;
val string_of_tree : char binary_tree -> string = <fun>

One can also use a buffer to allocate a lot less memory:

# let rec buffer_add_tree buf = function
    | Empty -> ()
    | Node (data, l, r) ->
       Buffer.add_char buf data;
       match l, r with
       | Empty, Empty -> ()
       | _, _ -> Buffer.add_char buf '(';
                 buffer_add_tree buf l;
                 Buffer.add_char buf ',';
                 buffer_add_tree buf r;
                 Buffer.add_char buf ')'
                 let string_of_tree t =
    let buf = Buffer.create 128 in
      buffer_add_tree buf t;
      Buffer.contents buf;;
val buffer_add_tree : Buffer.t -> char binary_tree -> unit = <fun>
val string_of_tree : char binary_tree -> string = <fun>

For the reverse conversion, we assume that the string is well formed and do not deal with error reporting.

# let tree_of_string =
    let rec make ofs s =
      if ofs >= String.length s || s.[ofs] = ',' || s.[ofs] = ')' then
        (Empty, ofs)
      else
        let v = s.[ofs] in
        if ofs + 1 < String.length s && s.[ofs + 1] = '(' then
          let l, ofs = make (ofs + 2) s in (* skip "v(" *)
          let r, ofs = make (ofs + 1) s in (* skip "," *)
            (Node (v, l, r), ofs + 1) (* skip ")" *)
        else (Node (v, Empty, Empty), ofs + 1)
    in
      fun s -> fst (make 0 s);;
val tree_of_string : string -> char binary_tree = <fun>

60. Preorder and Inorder Sequences of Binary Trees

We consider binary trees with nodes that are identified by single lower-case letters, as in the example of the previous problem.

1. Write functions preorder and inorder that construct the preorder and inorder sequence of a given binary tree, respectively. The results should be atoms, e.g. ‘abdecfg’ for the preorder sequence of the example in the previous problem.
2. Can you use preorder from problem part 1 in the reverse direction; i.e. given a preorder sequence, construct a corresponding tree? If not, make the necessary arrangements.
3. If both the preorder sequence and the inorder sequence of the nodes of a binary tree are given, then the tree is determined unambiguously. Write a function pre_in_tree that does the job.
4. Solve problems 1 to 3 using difference lists. Cool! Use the function timeit (defined in problem “Compare the two methods of calculating Euler’s totient function.”) to compare the solutions.

What happens if the same character appears in more than one node. Try for instance pre_in_tree "aba" "baa".

# preorder (Node (1, Node (2, Empty, Empty), Empty));;
- : int list = [1; 2]

经典前序中序。

没太理解 difference lists是怎么回事，看了维基也没太理解，O(1) 的连接效率，感觉就是个链表？是在说 @ 这种标准库带的连接方式 O(n) 吗。

可以传个 acc 防止列表连接的，我懒得搞了。

same character appears in more than one node会怎么样，会没法判断呗。

let rec preorder root = match root with
	| Empty -> []
	| Node(v,l,r) -> (v::preorder l)@preorder r

这种传啥都没用了。

let rec inorder root =  match root with
	| Empty -> []
	| Node(v,l,r) -> (preorder l)@[v]@preorder r

这里需要一个神秘的字符串切割。

let rec pre_in_tree pre in_order = if String.length pre != String.length in_order then raise Not_found else
	if String.length pre = 1 then Node(pre,Empty,Empty)
	else let pos = String.index_from in_order 0 pre.[0] in
	let remain = Str.string_after pre 1 in
	Node(String.make 1 pre.[0], pre_in_tree (Str.string_before remain pos) (Str.string_after remain pos), 
		pre_in_tree (Str.string_before in_order pos) (Str.string_after in_order (pos+1)));;

val pre_in_tree : string -> string -> string binary_tree = <fun>

很神秘哦，split_pre_in，我瞧瞧怎么回事。

你也偷懒是吧。

We use lists to represent the result. Note that preorder and inorder can be made more efficient by avoiding list concatenations.

# let rec preorder = function
    | Empty -> []
    | Node (v, l, r) -> v :: (preorder l @ preorder r)
    let rec inorder = function
    | Empty -> []
    | Node (v, l, r) -> inorder l @ (v :: inorder r)
    let rec split_pre_in p i x accp acci = match (p, i) with
    | [], [] -> (List.rev accp, List.rev acci), ([], [])
    | h1 :: t1, h2 :: t2 ->
       if x = h2 then
         (List.tl (List.rev (h1 :: accp)), t1),
         (List.rev (List.tl (h2 :: acci)), t2)
       else
         split_pre_in t1 t2 x (h1 :: accp) (h2 :: acci)
    | _ -> assert false
    let rec pre_in_tree p i = match (p, i) with
    | [], [] -> Empty
    | (h1 :: t1), (h2 :: t2) ->
       let (lp, rp), (li, ri) = split_pre_in p i h1 [] [] in
         Node (h1, pre_in_tree lp li, pre_in_tree rp ri)
    | _ -> invalid_arg "pre_in_tree";;
val preorder : 'a binary_tree -> 'a list = <fun>
val inorder : 'a binary_tree -> 'a list = <fun>
val split_pre_in :
  'a list ->
  'a list ->
  'a -> 'a list -> 'a list -> ('a list * 'a list) * ('a list * 'a list) =
  <fun>
val pre_in_tree : 'a list -> 'a list -> 'a binary_tree = <fun>

Solution using difference lists.

  (* solution pending *)

61. Dotstring Representation of Binary Trees

We consider again binary trees with nodes that are identified by single lower-case letters, as in the example of problem “A string representation of binary trees”. Such a tree can be represented by the preorder sequence of its nodes in which dots (.) are inserted where an empty subtree (nil) is encountered during the tree traversal. For example, the tree shown in problem “A string representation of binary trees” is represented as ‘abd..e..c.fg…’. First, try to establish a syntax (BNF or syntax diagrams) and then write a function tree_dotstring which does the conversion in both directions. Use difference lists.

好说，必定有子树了呗，反而更好处理递归了。

let rec tree_dotstring root = match root with
	| Empty -> "."
	| Node(v,l,r) -> v ^ (tree_dotstring l) ^ (tree_dotstring r)
;;
let parse_tree_dotstring str = 
	let rec aux s= 
	if String.length s = 0 then raise Not_found
	else if s = "." then (Empty, "")
	else let remain_str = Str.string_after s 1 in
		match s.[0] with
			| '.' -> (Empty, remain_str)
			| v -> let l_t,remain_str = aux remain_str in
				let r_t,remain_str = aux remain_str in
				(Node(v,l_t,r_t), remain_str)
	in
	fst (aux str)

答案又偷懒了，所以说 difference lists 的都没做是吗。

总结

二叉树结束了，树天然适合递归，比起不能取址的随机存取数组，递归用起来更加自然合适了。

多说一句，OCaml 的字符串处理是真的难搞啊，也有可能是我已经适应了新时代丰富的趁手库函数，丧失了自己随手造个好用轮子的猛男气概了。还有，切片真是个好东西啊。